Arithmetic » Number systems (sets)
Contents
Natural numbersIntegers or whole numbers
Rational or fractional numbers
Real numbers
Complex numbers
Natural numbers
A natural number is a number from the set 0, 1, 2, 3, 4, ...
The set of all natural numbers is indicated with symbol 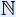 .
.
There is discussion about whether zero is part of 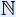 .
.
Nowadays zero is mostly part of the natural numbers.
When people do not begin the natural numbers with zero, they use 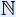 for the natural numbers excluding zero and
for the natural numbers excluding zero and 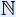 0 for the natural numbers including zero.
0 for the natural numbers including zero. 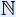 0 is then called the non-negative numbers.
0 is then called the non-negative numbers.
Integers or whole numbers
An integer is a number from the set ..., –4, –3, –2, –1, 0, 1, 2, 3, 4, ...
The set of all integers is indicated with symbol 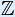 .
.
The Z comes from the German word 'Zahl', which means number.
The set 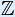 includes set
includes set 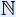 .
.
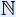 is therefore a subset of
is therefore a subset of 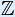 .
.
You may write this as 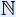 ⊂
⊂ 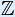 .
.
Rational or fractional numbers
A rational number is the quotient of two integers.
Therefore every number that can be written as a fraction (fractional or broken number) is a rational number.
The set of all rational numbers is indicated with symbol 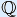 .
.
As every integer can be written as a fraction, 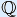 includes
includes 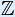 .
.
You may write this as 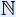 ⊂
⊂ 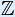 ⊂
⊂ 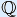 .
.
Real numbers
Besides rational numbers, there are also numbers that cannot be written as a fraction. For example 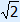 and π. Numbers that cannot be written as a fraction are called irrational numbers. The rational numbers and irrational numbers together form the set of real numbers.
and π. Numbers that cannot be written as a fraction are called irrational numbers. The rational numbers and irrational numbers together form the set of real numbers.
The real numbers make up all numbers on a number line.
The set of all real numbers is indicated with symbol 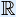 .
.
Because 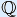 is a subset of
is a subset of 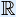 , we can write:
, we can write: 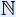 ⊂
⊂ 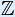 ⊂
⊂ 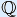 ⊂
⊂ 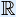 .
.
Complex numbers
Above you read that the real numbers form the numbers of a number line.
However, in some parts of science, there was a need for numbers in a plane. In other words: Two number lines. Complex numbers are invented because of this. A complex number is a combination of two real numbers a and b where a number is written as: a + bi. Here i is the imaginary unit where i2 = –1.
In this way you can show every number a + bi in a plane, where a is the number on the horizontal axis and bi is the number on the vertical axis.
The set of all complex numbers is indicated with symbol 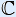 .
.
Because 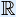 is a subset of
is a subset of 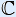 , we can write:
, we can write: 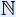 ⊂
⊂ 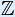 ⊂
⊂ 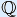 ⊂
⊂ 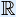 ⊂
⊂ 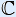 .
.
Watch out: x2 = –1 DOES have solutions with complex numbers.
As i2 = –1, the equation x2 = –1 has solutions x = –i or x = i.
This is because (–i)2 is also –1.
Example
| 3x2 + 50 | = 2 |
| 3x2 | = –48 |
| x2 | = –16 |
| x = –4i | or x = 4i |