Equations » Derivation of the quadratic formula
Below is explained how the quadratic formula / abc-formula is derived. Looking for the explanation and / or examples of the quadratic formula? You can find them at the theory about quadratic equations.
How do you work?
Every quadratic equation can be written as ax2 + bx + c = 0. As you want to know what x is, you should bring everything to the right-hand side of the =-sign. To get this, you shall have to take the square root of both sides to get rid of the square.
To get only x2 on the left is impossible. For that reason you try to write the left-hand side as p2 + 2pq + q2. With the rule p2 + 2pq + q2 = (p + q)2 you will get a nice square of which you can take the square root.
So you have to write the left hand side as p2 + 2pq + q2 so you are able to write it as (p + q)2. Take the square root of both sides and islolate the x and simplify the right hand side as far as possible.
The derivation
1: | ax2 + bx + c | = 0 |
2: | ax2 + bx | = –c |
3: | x2 + bax | = –ca |
4: | x2 + 2b2ax | = –ca |
5: | x2 + 2b2ax +  b2a b2a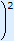 | =  b2a b2a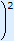 – ca – ca |
6: |  x + b2a x + b2a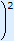 | =  b2a b2a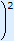 – ca – ca |
7: |  x + b2a x + b2a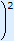 | = b24a2 – 4ac4a2 |
8: |  x + b2a x + b2a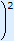 | = b2 – 4ac4a2 |
9: | x + b2a = 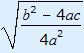 | or x + b2a = –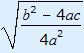 |
10: | x = –b2a +  2a 2a | or x = –b2a –  2a 2a |
11: | x = –b +  2a 2a | or x = –b –  2a 2a |
Bij substituting b2 – 4ac for D you will get (D = Discriminant):
x = –b + 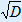 2a or x = –b –
2a or x = –b – 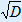 2a (with D = b2 – 4ac)
2a (with D = b2 – 4ac)
Explanation of the steps
1: | Initial equation. |
2: | Do – c on both sides. |
3: | Divide everything by a. |
4: | Rewrite ba to 2b2a so you second term will be 2pq. |
5: | Do +  b2a b2a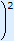 on both sides so you get q2 as the third term. on both sides so you get q2 as the third term. |
6: | Use p2 + 2pq + q2 = (p + q)2. |
7: | Simplify  b2a b2a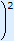 and change ca so the denominator is 4a2. and change ca so the denominator is 4a2. |
8: | Make one fraction. |
9: | Take the square root on both sides. Two solutions! |
10: | Do – b2a on both sides and use 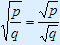 on the right-hand side. on the right-hand side. |
11: | Final answer. |