Equations » Enclosure method
Using the enclosure method to solve a maths problem is to systematically try and get the answer to an equation by filling in values into the formula. To solve an equation with the enclosure method, you best make a graph for your first estimate and then make a table to show which number is closest to your target. Always show the result just above and just below your target.
I will give two examples.
At the second example I will explain how you can calculate more decimals.
Example one formula
Given is the formula b = 3p2 + 4p.
Calculate to one decimal, for which p the outcome is b = 150.
Answer
Plot the graph and search the point where b = 150.
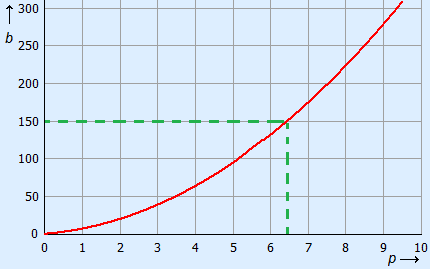
It seems that is at p = 6.3.
Make a table and use for p numbers just above and below your estimation.
| p | 6.1 | 6.2 | 6.3 | 6.4 | 6.5 | |
| b | 136.0 | 140.1 | 144.3 | 148.5 | 152.8 | |
| difference with 150 | 14.0 | 9.9 | 5.7 | 1.5 | 2.8 |
In the table b = 148.5 is closest to 150, so the solution is p ≈ 6.4.
This question could also be solved algebraically by solving the equation 3p2 + 4p = 150.
Example two formulas
Karel and Tom both let their model plane take off. The height h in metres of the planes after t seconds can be calculated with the following formulas.
Karel: h = 0.1t2 + 0.1t
Tom: h = 0.021t3
Calculate after how many seconds the planes have the same height. Round to one decimal.
Answer
Plot the graphs in one coordinate system and estimate the value of t of the point of intersection.
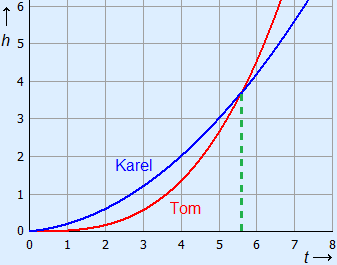
It seems that is at t = 5.7.
Make a table and use for t numbers just above and below your estimation.
| t | 5.5 | 5.6 | 5.7 | 5.8 | 5.9 | |
| Karel: h = 0.1t2 + 0.1t | 3.58
| 3.70 |
3.82 |
3.94 |
4.07 |
| |
| Tom: h = 0.021t3 | 3.49 | 3.69 | 3.89 | 4.10 | 4.31 | |
| difference | 0.09 | 0.01 | 0.07 | 0.16 | 0.24 |
I always indicate which numbers are bigger after I have made the table. Above I did this by making them bold, but on paper I often underline them. This way it is easier to see between which two values the point of intersection lies, namely between t = 5.6 and t = 5.7. The difference is smallest at t = 5.6, so the solution is t ≈ 5.6.
More decimals?When more decimals are asked, you will have to make another table in which you work with more decimals. Let's say that we need more decimals for the example above. We know that the point of intersection is between t = 5.6 and t = 5.7. Furthermore, because of the small difference we just saw at t = 5.6, we know that this will be just after 5.6. So we make a table with 5.60, 5.61, 5.62. When needed you can always make the table longer as you go with 5,63, etcetera. Note that you might have to give the results in more decimals as well.
| t | 5.60 | 5.61 | 5.62 | ||
| Karel: h = 0.1t2 + 0.1t | 3.696
| 3.7082 |
3.720 |
|
| |
| Tom: h = 0.021t3 | 3.688 | 3.7077 | 3.728 | ||
| difference | 0.008 | 0.0005 | 0.008 |
The solution is t ≈ 5,61.
It was not necessary to give the fourth decimal for the results of t = 5,61 in the table above. But if you need more decimals for your solution you now know that the point of intersection is between t = 5.61 en t = 5.62. You will have to make a new table with t numbers between 5.61 and 5.62.