Equations » Fractional equations
To solve a fractional equation you have to remove the fraction by multiplying both sides of the equation with the denominator(s).
Important: Check your solutions. Perhaps a solution will not have an outcome in the original equation. See example 4.
Example 1 with the card method
| 1202x – 9 | = 24 |  card method: card on 2x – 9 card method: card on 2x – 9 |
| 2x – 9 | = 5 | |
| 2x | = 14 | |
| x | = 7 |
Example 1 with multiplying by the denominator
| 1202x – 9 | = 24 |  both sides times (2x – 9) both sides times (2x – 9) |
| 120 | = 24(2x – 9) | |
| 120 | = 48x – 216 | |
| 336 | = 48x | |
| x | = 7 |
Example 2
| 3 – 5xx + 3 | = –2 |  both sides times (x + 3) both sides times (x + 3) |
| 3 – 5x | = –2(x + 3) | |
| 3 – 5x | = –2x – 6 | |
| 3 – 5x | = –6 | |
| –3x | = –9 | |
| x | = 3 |
Example 3
| x + 13x – 2 | = x – 3 |  both sides times (x – 2) both sides times (x – 2) |
| x + 13 | = (x – 3)(x – 2) | |
| x + 13 | = x2 – 5x + 6 | |
| –x2 + 6x + 7 | = 0 | |
| x2 – 6x – 7 | = 0 | |
| (x + 1)(x – 7) | = 0 | |
| x = –1 or x = | 7 |
Example 4
| 12x + 3 | = 3x2x + 6 |  cross products cross products |
| 12(2x+ 6) | = 3x(x + 3) | |
| 24x + 72 | = 3x2 + 9x | |
| –3x2 + 15x + 72 | = 0 | |
| x2 – 5x – 24 | = 0 | |
| (x – 8)(x + 3) | = 0 | |
| x = 8 of x = | –3 |
When we fill in x = –3 into the original equation we will get no outcome because you will get a division by zero. Therefore only x = 8 is the solution.
Example 5
| 6x2 – 12x2 – 12 | = 0 |  card method: de numerator must be 0! card method: de numerator must be 0! |
| 6x2 – 12 | = 0 | |
| 6x2 | = 12 | |
| x2 | = 2 | |
x = 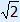 | or x = –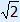 |
Example 6
| xx – 1 + 2x + 1 | = 2 |  both sides times (x – 1) both sides times (x – 1) both sides times (x + 1) both sides times (x + 1) |
| x + 2(x – 1)x + 1 | = 2(x – 1) | |
| x(x + 1) + 2(x – 1) | = 2(x – 1)(x + 1) | |
| x2 + x + 2x – 2 | = 2(x2 – 1) | |
| x2 + 3x – 2 | = 2x2 – 2 | |
| –x2 + 3x | = 0 | |
| –x(x – 3) | = 0 | |
| x = 0 or x = | 3 |
Example 7
| x2 – 16x2 + 3x – 4 | = x20 | |
| (x + 4)(x – 4)(x + 4)(x – 1) | = x20 | |
| x – 4x – 1 | = x20 |  cross products cross products |
| x(x – 1) | = 20(x – 4) | |
| x2 – x | = 20x – 80 | |
| x2 – 21x + 80 | = 0 | |
| (x – 5)(x – 16) | = 0 | |
| x = 5 or x = 1 | 6 |