Equations » Power equations
A power formula is always of the form y = axb.
A power equation is always of the form axb = c.
One or two solutions?
A power equation always has one solution when you have an odd exponent.
A power equation has two, one or zero solutions when you have an even exponent.
Think of a quadratic equation (even exponent):
x2 = 4 has two solutions, namely x = –2 or x = 2.
x2 = 0 has one solution, namely x = 0.
x2 = –1 has no solutions.
Root = power
Every root can be written as a power.
The rule is 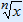 = x
= x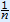 .
.
Example 1
| 3x4 + 8 | = 1883 |
| 3x4 | = 1875 |
| x4 | = 625 |
x = –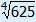 | of x = 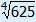 |
| x = –5 | or x = 5 |
Example 2
| 500 – 2x5 | = 14 |
| 2x5 | = 486 |
| x5 | = 243 |
| x | = 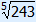 = 3 = 3 |
Example 3
| 7x3 + 6 | = –204 |
| 7x3 | = –210 |
| x3 | = –30 |
| x | = 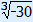 ≈ –3.107 ≈ –3.107 |
Example 4
On the graph of y = 112x0.43 lies point (x; 14.5).
Calculate x. Round to 4 decimals.
| 14.5 = | 112x0.43 |
| x0.43 = | 14.5112 |
| x = |  14.5112 14.5112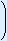 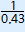 ≈ 0.0086 ≈ 0.0086 |