Formulas, graphs & relations » Mutations on formulas and graphs (translating and stretching)

1. Translation (addition)
2. Stretching (multiplication)

1. Translation (addition)

You can change a graph by moving it vertically or horizontally. This is called translation.

Vertical translation (up/down)

To translate a formula vertically with q, you just add + q behind the formula. When translating down q is negative. To plot the new graph from the old graph is easy. Just read off every value, add q and plot the new graph.

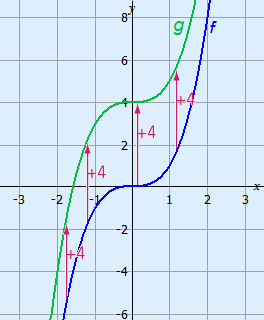
Example
Below you can see how function f (x) = x³ is translated upwards by 4.
The function for the new graph is g(x) = x³ + 4.
Graph that is translated upwards by 4

Horizontal translation (left/right)

When translating a formula or graph horizontally to the right with p, you change every x in the old formula with (x – p).
When translating left p is negative. In that case you will get (x – (–…)) = (x + …).
For the graphs it works the same as above, only now you have to read off every point and you will have to plot the new points p to the right.

Example
The function f (x) = 2x² + 3x is translated 5 units to the left.
The new function is g(x) = 2(x + 5)² + 3(x + 5).
By removing brackets you will get:

`g`(`x`) =	2(`x` + 5)² + 3(`x` + 5)
	2(`x` + 5)(`x` + 5) + 3`x` + 15
	2(`x`² + 10`x` + 25) + 3`x` + 15
	2`x`² + 20`x` + 50 + 3`x` + 15
	2`x`² + 23`x` + 65.

Vertical and horizontal

For a translation to the right with p and upwards with q, you will get translation (p, q).
For the standard formula y = axⁿ then new formula will be: y = a(x – p)ⁿ + q.

2. Stretching (multiplication)

You can change a graph by multiplying it with a certain number. This is called stretching.

Stretching parallel to the `y`-axis

When stretching parallel to the y-axis with a factor a all outcomes of a formula are multiplied with a. The graph will be a times further from the x-axis.

The new formula can be easily found:
new formula = a(old formula).
Mind the brackets around the old formula!

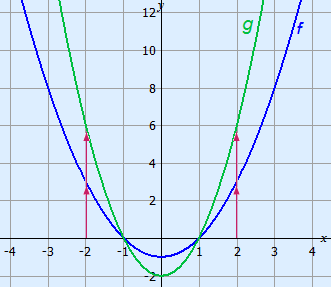
Example
The graph of function f (x) = x² – 1 is stretched parallel to the y-axis with factor 2.
All points of the new graph will be twice as far from the x-axis.
The function of the new graph will be g(x) = 2(x² – 1) = 2x² – 2.
Graphs of a parabola stretched parallel to the y-axis with 2

Stretching parallel to the `x`-axis

When stretching parallel to the x-axis with factor a you substitute every x elke x in the function by (1ax).

When plotting the new graph it works the same, now the new points will have to be a times further from the y-axis.

Example
The function f (x) = 3x² + 5x – 2 is stretched parallel to the x-axis with factor 4.

The new function will be `g`(`x`)=	3(14`x`)² + 5(14`x`) – 2
=	3(14)²`x`² + 54`x` – 2.
=	3 × 116 × `x`² + 114`x` – 2.
=	316`x`² + 114`x` – 2.

To top