Geometry » Calculating area of compound figures
Calculating the area of a compound figure works as follows:
| 1. | Divide the figure into known figures like rectangle and (semi-)circles. |
| 2. | Calculate the area of the separate figures. |
| 3. | Calculate the area of the whole figure by adding the area of the separate figures. |
Example
Calculate the area of the following figure in m2.
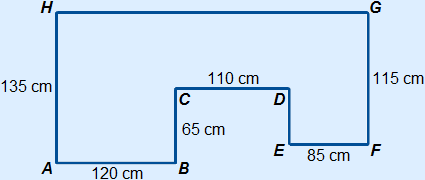
Divide the figure into separate figures. In this case three rectangles.
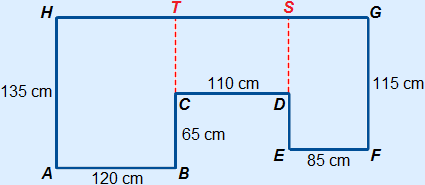
To calculate all the areas, we need the length of CT (or DS).
CT = DS = 135 – 65 = 70 cm
Now we can calculate the areas.
Area rectangle left = 120 × 135 = 16200 cm 2
Area rectangle middle = 110 × 70 = 7700 cm2
Area rectangle right = 85 × 115 = 9775 cm2
Area whole figure = 16200 + 7700 + 9775 = 33675 cm2 = 3,3675 m2
Other method
The figure can also be divided into other rectangles.
Below, you can see one of these ways.
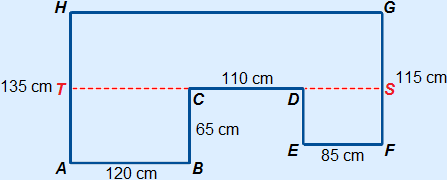
However, this method gives us more unknown sides that we need. We now need HT (or GS), GH (or ST) and DE (or FS) before we can calculate the areas.
HT = GS = 135 – 65 = 70 cm
GH = ST = 120 + 110 + 85 = 315 cm
DE = FS = 65 - (135 - 115) = 45 cm
Now we can calculate the areas.
Area rectangle ABCT = 120 × 65 = 7800 cm 2
Area rectangle TSGH = 315 × 70 = 22050 cm2
Area rectangle EFSD = 85 × 45 = 3825 cm2
Area whole figure = 7800 + 22050 + 3825 = 33675 cm2 = 3,3675 m2