Geometry » Circles
What is a circle?
The definition of a circle is:
A set of points in a plane that are equidistant to a given point, the centre.
The blue line in the drawing below is the circle. So not the area within.
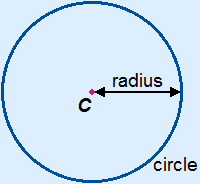
The distance between the centre and the circle is called the radius*1.
The distance circle-circle through the centre is called the diameter.
The perimeter of the circle is called the circumference.
Calculating with circles
diameter = 2 × radius
radius = 12 × diameter (or diameter : 2)
area circle*2 = radius × radius × π
circumference = diameter × π
In letters and as short as possible:
d = 2r
r = 12d
A = πr2
C = dπ
| *1 | The plural form of radius is radii. |
| *2 | With the area of the circle, we mean the area enclosed by the circle. The area within the circle is actually called a disc. |
Other lines and areas
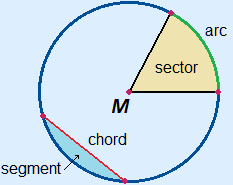
Above, you learned the following terms already:
radius (radii), diameter and disc.
You also have:
arc - a part of a circle.
chord - the line segment that connects two points on a circle.
sector - the area enclosed by an arc and both radii to the ends of the arc.
segment - the area enclosed by an arc and its corresponding chord.