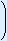Geometry » Coordinates
Contents
2D coordinates3D coordinates
Cartesian coordinate system
Polar coordinates
Spherical coordinates
2D coordinates
To the right you can see a coordinate system with a number of points. You always first read off the horizontal coordinate. In this case on the x-axis. Then you read off the vertical coordinate. In this case the y-axis. These two coordinates are always separate by a comma. So (x, y). If the point has a name (a capital letter) you write it immediately in front of the first bracket. Use no marks/signs between the capital letter and the first bracket.
The first five points in this coordinate system have the following coordinates:
| A(2, 0) | B(2, 4) | C(5, 2) | D(7, 0) | E(0, 7) |
Broken numbers:
If you have a point that is not on a grid point and the x-coordinate is therefore for example 1.5 make sure you make a legible difference between your decimal dot(s) and the comma.
You can also choose to write fractions instead of decimal numbers.
In countries where a decimal comma is used, the semicolon ( ; ) is used instead of the comma to separate the two coordinates.
| Countries using a decimal dot: F(6.5, 5) or F(612, 5) G(4.5, 6.5) or G(412, 612) |
Countries using a decimal comma: F(6,5; 5) or F(612, 5) G(4,5; 6,5) of G(412, 612) Note: The semicolon can always be used. Even if there are no decimal numbers. |
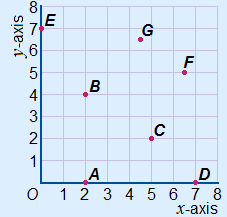
3D coordinates
Just like you can use coordinates to indicate locations in a 2D coordinate system, you can also indicate points in space with a 3D coordinate system.
The only thing we need is another axis. This axis is called the z-axis. With this extra axis you have a xyz-system. See the drawing.
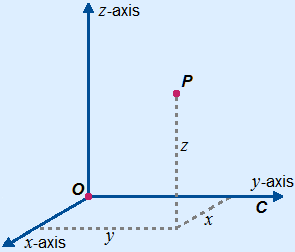
Indicating a point on the cube is done in almost the same way as in a 2D coordinate system. The coordinates are between brackets and separated by a comma ( , , ) or a semicolon ( ; ; ).  The coordinates are written in this order: (x , y , z)
The coordinates are written in this order: (x , y , z)
The coordinates of E are E(4, 0, 4).
You first go 4 steps towards the front, always starting in the origin. That is the x-coordinate. You are in point A then. Next you are going 0 steps towards the right, that is the y-axis. So you stay in point A. Finally you go 4 steps upwards, that is the z-axis. You arrived in point E.
Cartesian coordinate system
The ways to use coordinates described above are Cartesian coordinates. They are called like this because of the Cartesian coordinate system in which they are applied.
A Cartesian coordinate system is sometimes called a rectangular coordinate system.
The coordinate system is orthogonal. So, the distance between two adjacent coordinate lines is equal.
Other forms of coordinate systems are those with slanted axes or polar coordinates. The 3D system of polar coordinates are called spherical coordinates. These are explained below.
Polar coordinates
A location in a plane can also be determined by polar coordinates.
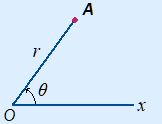 As the base / reference point again we use O.
As the base / reference point again we use O.
This is called the pole.
There also is a polar axis extending rightwards from the pole.
Polar coordinates have the form (r, θ).
r is the distance to the pole.
θ (theta) is the angle from the polar axis.
Other symbols:
Instead of r sometimes the ρ (rho) is used.
Instead of θ sometimes the φ (phi) is used.
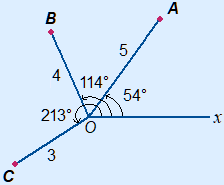
When the distance OA = 5 and the angle between the polar axis and OA are 54°, then the polar coordinates of point A are A(5, 54°).
From the degree symbol you can make up that you are handling polar coordinates.
Are you working with radians? Then you have a decimal number or the symbol π.
Below you can find the points A(5, 54°), B(4, 114°) and C(3, 213°)
Converting polar coordinates en Cartesian coordinates
Polar coordinates to Cartesian coordinates:
x = r cos(θ)
y = r sin(θ)
Cartesian coordinates to polar coordinates:
r = 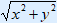
θ = tan-1 yx
yx
Sometimes tan-1 is written as arctan.
Watch out: tan-1 only gives answers between –90° and 90° or –12π and 12π radians.
When x is not positive you will have to some arithmetic to get the right answer.
| x ≤ 0 | degrees | radians |
| x = 0 and y > 0 | 90° | 12π |
| x = 0 and y < 0 | 270° or –90° | 112π or –12π |
| x < 0 and y = 0 | 180° | π |
| x < 0 and y > 0 | + 180° | + π |
| x < 0 and y < 0 | – 180° | – π |
Graphical calculator
On the graphical calculator converting is often possible as a function.
On the Texas Instruments you have the following functions in the ANGLE menu:
R►Pr( R►Pθ( P►Rx( P►Ry(
The R stands for rectangular, thus the Cartesian coordinates.
Behind the ( you have to key in the (polar) coordinates you want to convert, of course separated by a comma.
Spherical coordinates
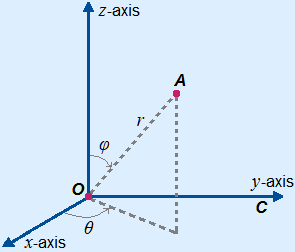 Spherical coordinates are the three dimensional system of polar coordinates.
Spherical coordinates are the three dimensional system of polar coordinates.
Spherical coordinates have the form (r, φ, θ).
r is the distance to the pole.
φ is the angle between OA and
the positive z-axis.
θ is the angle in the xy-plane.
With physics φ and θ are usually swapped ...
The second coordinate is then also the angle between OA and the positive z-axis, so not a big problem.
Converting spherical coordinates and Cartesian coordinates
Spherical coordinates to Cartesian coordinates:
x = r sin(φ) cos(θ)
y = r sin(φ) sin(θ)
z = r cos(φ)
Cartesian coordinates to spherical coordinates:
r = 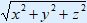
φ = cos-1 zr
zr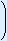 =
= cos-1 z
z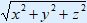
θ = tan-1 yx
yx