Geometry » Quadrilaterals
Contents
- Scalene or irregular quadrilateral- Square
- Rectangle
- Parallelogram
- Kite
- Rhombus
- Trapezium (US: Trapezoid)
How does the set of quadrilaterals relate to each other?
Scalene or irregular quadrilateral
A quadrilateral without any special properties. There is no symmetry and there are no lines parallel or perpendicular to each other.
Square (regular quadrilateral)
A square is a quadrilateral with four equal sides and four equal angels.
The diagonals intersect perpendicularly and bisect each other.
The diagonals are equally long.
There are two pairs of equal sides.

| Area | = length × width |
| = side × side | |
| = side2 |
Rectangle
A quadrilateral with four right angles (90°).
In a rectangle the diagonals bisect each other.
The diagonals are equally long.
Area = length × width
Parallelogram
A quadrilateral with rotation symmetry.
A quadrilateral with two pairs of parallel lines.
The opposite sides are equal in length (and parallel).
The opposite angles are equal in size.
The diagonals cut each other into two equal parts.

Area = base × height
Example
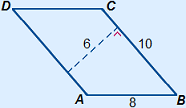
Base and height always are perpendicular to each other.
Area ABCD = 10 × 6 = 60
Kite
A kite is a quadrilateral where a diagonal is an axis of symmetry.
Two by two the sides are equal in length.
The diagonals intersect perpendicularly.
Two angles have the same size.
Area = length diagonal PR × length diagonal QS : 2
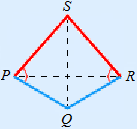
Example
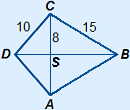
We need the length of both diagonals.
AC = 2 × 8 = 16
The length of BD is not given, so we need to calculate it.
We can do this with Pythagoras' theorem.
DS = |
BS = | |||||||||||||||||||||||||||||||||
BD = DS + BS = 6 + 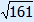
Area ABCD = AC × BD : 2 = 16 × (6 + 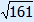 ) : 2 ≈ 149.5
) : 2 ≈ 149.5
Rhombus
A rhombus is a quadrilateral with four equal sides.
A rhombus is a quadrilateral where both diagonals are axes of symmetry.
The opposite angles are equal in size.
The diagonals intersect perpendicularly and bisect.
The diagonals divide the angles into two equal parts (angle bisector).
Area = see kite
Trapezium (US: trapezoid)
A quadrilateral with one pair of parallel lines.
No special properties.
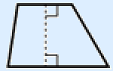
Area = (length small base + length large base) × height : 2
Example
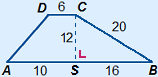
Base and height always are perpendicular to each other.
AB = AS + BS = 10 + 16 = 26
Area ABCD = (AB + CD) × CS : 2 = (26 + 6) × 12 : 2 = 192
Isosceles trapezium
When the base angles in a trapezium are equal, the trapezium is isosceles.
Has one axis of symmetry.
Has two pairs of equal angles.
Two sides (drawn blue underneath) are equal in length.
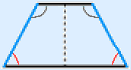
Area = See trapezium
How does the set of quadrilaterals relate to each other?
See the figure below:
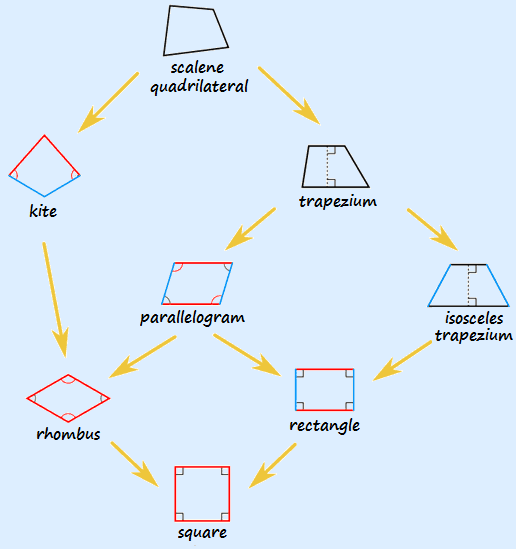
A square is a special rectangle.
A square is a special rhombus.
A square is a special parallelogram.
A square is a special kite.
A square is a special trapezium.
A rectangle is a special parallelogram.
A rectangle is a special trapezium.
A rhombus is a special parallelogram.
A rhombus is a special kite.
A rhombus is a special trapezium.
A parallelogram is a special trapezium.
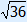 = 6
= 6