Geometry » Similarity

Contents

1. When are two figures similar?
2. Special case: the triangle
3. Examples
3. More examples (beak and hourglass figure)

1. When are two figures similar?

Two figures are similar when:
- the corresponding angles are equal in size
and
- the corresponding sides have the same scale factor.

An enlargement is always similar to the original.
If figure B is an enlargement of A, you may assume that figure A and B are similar.

Example:
Are the quadrilaterals below similar?
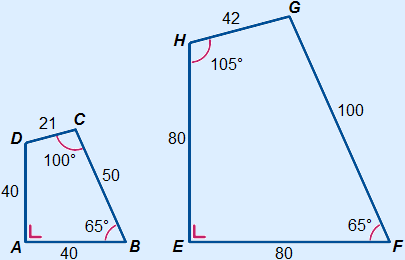
two quadrilaterals with different measurements, these will get given below

Are the corresponding angles equal?
angle signA = angle signE = 90°
angle signB = angle signF = 65°
angle signC = angle signG = 360° – 90° – 65° – 105° = 100°
angle signD = angle signH = 360° – 90° – 65° – 100° = 105°

Are the scale factors equal?
80 : 40 = 2
80 : 40 = 2
42 : 21 = 2
100 : 50 = 2

Both conditions are met, so yes, quadrilateral ABCD is similar to quadrilateral EFGH.


2. Special case: the triangle

A special case is the triangle. Because this shape has only three sides you need less information to draw a triangle. If you know one angle and two sides, you can already draw the triangle. This results in the fact that not both the similarity rules have to apply before you know that to figures are similar. If only one of the similarity rules apply, you already know for certain that the two triangles are similar.

Two triangles are similar when:

- the corresponding angles are equal in size (two is actually also sufficient, as the third angle always has to make 180°)
or
- the corresponding sides have the same scale factor.

Examples

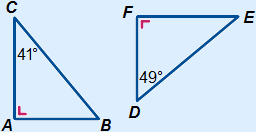Triangle ABC with angle A=90° and angle C=41° and triangle DEF with angle D=49° and angle F=90°
Is ΔABC similar to ΔDEF?
angle signA = angle signF = 90°
angle signB = angle signD = 180° – 90° – 41° = 49°
Always write the third angle as well:
angle signC = angle signE = 180° – 90° – 49° = 41°

Conclusion:
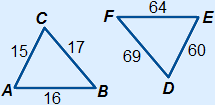Angles are equal, the triangles are similar. 		Triangle ABC with AB=15, BC=17 and AC=16 and triangle DEF with DE=64, EF=60 and DF=69
Is ΔABC similar to ΔDEF?
60 : 15 = 4
64 : 16 = 4
69 : 17 = 4117

Conclusion:
Scale factors are different, so the figures are not similar.

3. Examples

Example 1
See the figure below.
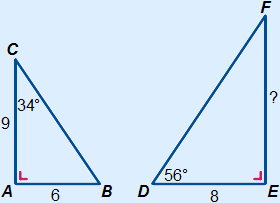
Triangle ABC with AB=6, AC=9, angle A=90° and angle C=39° and triangle DEF with DE=8, angle D=90° and angle D=51°
Calculate EF.

Answer:
Triangle ABC is similar to triangle EDF (letters on the same place as the corresponding angles), because:
angle signA = angle signE = 90°
angle signB = angle signD = 180° – 90° – 34° = 56°
angle signC = angle signF = 180° – 90° – 56° = 34°

The scale factor is 8 : 6 = 113.
Remember: NEVER round off scale factors, use a fraction instead!
EF = 9 × 113 = 12

Example 2
See the figure below.
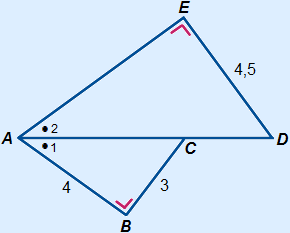
Triangle ABC with AB=4, BC=3, angle B=90° and triangle ADE with DE=4,5 and angle E=90°. It is known that angle BAC = angle DAE
Calculate AE and AD.

Answer:
Triangle ABC is similar to triangle AED, because:
angle signA1= angle signA2
angle signB = angle signE
The scale factor is is 4.5 : 3 = 1.5.
You need Pythagoras' theorem to calculate AC.
AC = 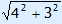square root(4^2 + 3^2) = 5, you may also use a scheme to calculate AC.
AE = AB × 1.5 = 4 × 1.5 = 6
AD = AC × 1.5 = 5 × 1.5 = 7.5

4. More examples

Example 1 contains a beak figure.
Example 2 contains an hourglass figure.

Example 1
See the figure below.
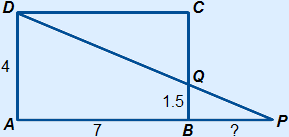
Rectangle ABCD with P on the extended line AB and Q the intersection of line DP with line BC. AB=7, BQ=1.5 and AD=4
Given is that ABCD is a rectangle.
Calculate BP.

Answer:
Triangle DQC is similar to triangle BPQ, because:
angle signD2 = angle signP (because of Z-angle, check angles)
angle signC = angle signB = 90° (rectangle)
The scale factor is (4 – 1.5) : 1.5 = 123.
BP = CD : 123 = 7 : 123 = 415

Note: You can also use triangle APD, but in that case you need to solve an equation to get to you answer. See also example 3.

Example 2
See the figure below.
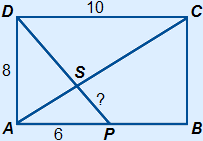
Ractangle ABCD with P on side AB and point S the intersection of AC and DP. AP=6, AD=8 and CD=10
Given is that ABCD is a rectangle.
Calculate PS.

Answer:
Triangle APS is similar to triangle CSD, because:
angle signA2 = angle signC2 (because of Z-angle)
angle signP1 = angle signD2 (because of Z-angle)
The scale factor is 10 : 6 = 123.

We need to calculate PS, but you cannot do that straight away.
What we do know of PS is the following:
PS + DS = PD
DS = 123 × PS

PD can be calculated using Pythagoras = 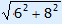square root(6^2 + 8^2) = 10 cm.
You may also use a scheme to calculate PD.

With the data above, we can change the formula to an equation:
(you subsitute DS = 123 × PS and PD = 10 into the formula)

PS + DS = PD
 PS + 123 × PS = 10
223PS = 10
 PS = 10 : 223 = 334 cm


To top