Geometry » Symmetry

Reflection symmetry/mirror symmetry/line symmetry

A figure has reflection symmetry when it consists of two halves that are each others mirror image. You can fold the figure in such a way that these halves go exactly on top of each other. This folding line is called the axis of symmetry.

Examples

Heart
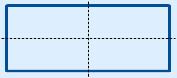1 axis of symmetry		  Rectangle 
2 axes of symmetry

Rotation symmetry

If you can rotate a figure in such a way that it exactly fits on itself again, this figure has rotation symmetry.
Note: The smallest rotation angle can never be bigger than 180°. The heart above has no rotation symmetry. The rectangle does have rotation symmetry. With a rotation of 180° it will be exactly the same figure.

Examples, including the smallest possible rotation angle

Wool mark sign
120°		 quadrialeteral with four right angles and slightly bent inwards sides
90°

If a figure has rotation symmetry with an angle of 180°, the figure is also point symmetrical. Point symmetry can also be called origin symmetry.
Both right-hand figures above are point symmetrical, because with a rotation over 180° the figure will be the same again. The wool mark sign (on the left) has no rotation symmetry over 180° so it is not point symmetrical.


There are more forms of symmetry, see wikipedia.