Inequalities » Linear inequalities
Check what is an inequality if you do not know what an inequality is.
Of course it is important to know what all the signs mean.
Check domain and range if your forgot what <, >, ≤ and ≥ mean.
Contents
1. Direction of sign afterwards2. Direction of sign during solving
1. Direction of sign afterwards
Steps:
| 1. | Make an equation that corresponds to the inequality. |
| 2. | Solve this equation. |
| 3. | Use a sketch or calculation(s) to decide the solution for the inequality. |
| 4. | Write the solution of the inequality. |
Example 1
| 8a + 4 | < 5a + 16 |
| 8a + 4 | = 5a + 16 |
| –4 | –4 |
| 8a | = 5a + 12 |
| –5a | –5a |
| 3a | = 12 |
| :3 | :3 |
| a | = 4 |
| Continue with sketch | Continue with calculations/number line | ||||||||||||
The gradients (8 and 5) tell us we have two rising lines.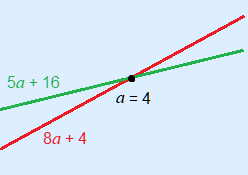 Look at the original inequality: 8a + 4 < 5a + 16 In the sketch you see that to the left of the point of intersection the outcomes of the red formula will be less than the green formula! Therefore, the inequality is true for values less than a = 4. Solution: a < 4 |
Calculate whether the inequality is correct for values to the left and right of the point of intersection. Left of the point of intersection: Take for example a = 3:
To the right of the point of intersection: Take for example a = 5:
You can make a sketch of a number line to help you.  Because to the left of the point of intersection is correct, all values less than a = 4 must be correct. Solution: a < 4 |
Example 2
| –3w + 7 | < 9w + 67 |
| –3w + 7 | = 9w + 67 |
| –7 | –7 |
| –3w | = 9w + 60 |
| –9w | –9w |
| –12w | = 60 |
| :–12 | :–12 |
| w | = –5 |
| Continue with sketch | Continue with calculations/number line | ||||||||||||
The gradients (–3 and 9) tell us we have a falling an a rising line.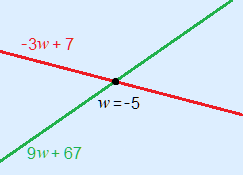 Look at the original inequality: –3w + 7 < 9w + 67 In the sketch you see that to the right of the point of intersection the outcomes of the red formula will be less than the green formula! Therefore, the inequality is true for values greater than w = –5. Solution: w > –5 |
Calculate whether the inequality is correct for values to the left and right of the point of intersection. Left of the point of intersection: Take for example w = –6, je krijgt dan
To the right of the point of intersection: Take for example w = –4, je krijgt dan
You can make a sketch of a number line to help you. 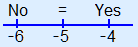 Because to the right of the point of intersection is correct, all values greater than w = –5 must be correct. Solution: w > –5 |
2. Direction of sign during solving
This method is faster, as it is less work. However, you make a mistake much more easily. You easily forget to apply the rule and you often do not check your answer at the end. This method can only be used when there is one solution for the equation.
The rule:
When multiplying or dividing with a negative number because of the balance method, the sign changes direction.
And:
When you swap your inequality, so you change the right-hand side of the inequality to be the left-hand side and vice versa, the sign also changes direction!
Examples
|
| ||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||