Probability » Product rule

Contents

1. Without replacing
2. With replacing
3. Combination of sum- and product rule

1. Without replacing

The product rule can be used with compound probability experiments, in which the probabilities do not remain the same.

Example
Given is the vase below with 4 red and 6 blue marbles.

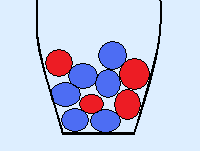
I take one marble marble without replacing it and repeat this another time.
What is the probability of getting two red marbles?

Answer:
The probability of getting a red marble the first time is 410.
There is a total of 10 marbles, of which 4 are red.
But the second time, the probability is not 410 anymore.
There is a total of 9 marbles, of which 3 are red. The probability is therefore 39.
The probability of taking two red marbles is 410 × 39 = 215.

2. With replacing

The product rule is especially handy when the probabilities do not change while doing the experiment.
The different events have to be independent of each other.
The possibilities can then be calculated using powers.
The following two examples show this:

Example 1
Given is the vase below with 4 red and 6 blue marbles.

I take one marble and replace it and repeat this another two times.
What is the probability of getting three red marbles?

Answer:
The probability to get a red marble is always 410, because the marbles are always put back in the vase.
The probability to get three red marbles is therefore 410 × 410 × 410 = (410)³ = 641000 = 8125.

Example 2
What is the probability of throwing a 4 three times and throwing an odd number seven times when you throw ten times with a regular 6-faced dice?

Answer:
The events are independent. The probability of throwing a 4 is 16. The probability of throwing an odd number is 12. The probability of throwing a 4 three times and throwing an odd number seven times is therefore: (16)³ × (12)⁷.
There are 10 nCr 3 possible orders of three times a 4 and seven times an odd number.
P(three times a 4 and seven times odd) = 10
3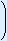(16)³(12)⁷ ≈ 0.004

3. Combinations of sum- and product rule

The product rule can also be used if you repeat a probability experiment over and over.

Example
Calculate the probability of having one 4 when you rotate five times with the following disc:


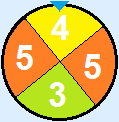
Answer:
The 4 can be gotten at the first OR the second OR the third OR the fourth OR the fifth try.
The probability can be calculated like this:
The first try: 14 × 34 × 34 × 34 × 34 = 811024
The second try: 34 × 14 × 34 × 34 × 34 = 811024
The third try: 34 × 34 × 14 × 34 × 34 = 811024
The fourth try: 34 × 34 × 34 × 14 × 34 = 811024
The fifth try: 34 × 34 × 34 × 34 × 14 = 811024
These probabilities have to be added to get the answer: 5 × 811024 = 4051024
The probability can also be calculated like this:  5
1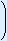(14)(34)⁴ = 4051024

To top