Rekenen » Romeinse, binaire, octale en Babylonische getallen

Ben je op zoek naar onze normale getallen? Kijk bij het decimale stelsel.

Inhoud

Romeinse getallen
Binaire getallen
Octale getallen (Het land van Oct)
Babylonische getallen
Optellen in de andere positiestelsels

Romeinse getallen

Het Romeinse talstelsel is het bekendste getalsysteem wat geen positiestelsel is. Het is namelijk een additief stelsel. Additief betekent toevoeging. Het systeem kent geen teken voor nul en ook geen negatieve getallen.

Symbool	Waarde	Waarde als getal
I	één	1
V	vijf	5
X	tien	10
L	vijftig	50
C	honderd	100
D	vijfhonderd	500
M	duizend	1000

Eerst maar eens het rijtje van 1 t/m 10:
I, II, III, IV, V, VI, VII, VIII, IX, X

De oorspronkelijke regels zijn dat je de waarde van losse symbolen bij elkaar optelt tenzij een symbool lager in waarde vóór een symbool hoger in waarde staat. Dan moet je de lagere waarde aftrekken van de hogere waarde. Ook mogen V, L en D maar maximaal één keer in het getal gebruikt worden. De getallen staan van hoog naar laag.
Later zijn daar de volgende regels aan toegevoegd om een eenduidig systeem te krijgen:
- Hooguit drie keer hetzelfde symbool achter elkaar.
- Hooguit één lager symbool voor een hoger symbool.
En deze twee regels die niet altijd even nauw genomen worden:
- V, L en D worden niet gebruikt om af te trekken, dus niet VC maar XCV.
- Een symbool mag alleen afgetrokken worden van een symbool dat vijf of tien keer zo groot is. IC mag niet, maar moet worden geschreven als XCIX

Nog wat voorbeelden:

Waarde	Romeins getal
78	LXXVIII
1244	MCCXLIV
2021	MXXI
1987	CMLXXXVIII

Uitzondering: Het getal vier

Op klokken zie je vaak IIII staan in plaats van IV voor vier. De meest gehoorde verklaring is dat IV de beginletters waren van Jupiter wat als IVPITER werd geschreven en daarom niet gebruikt. Een andere verklaring is dat IV vaak op zijn kop op de klok staat, het wordt dan snel verward met VI. Ook geeft IIII op een klok een mate van symmetrie. IIII is immers zo breed als VIIII. Je hebt dan ook I, II, III, IIII (= vier tekens met I), V, VI, VII, VIII (= vier tekens met V) en IX, X, XI, XII (= vier tekens met X).

Grootste Romeinse getal

Als je je strikt aan de regels houdt, mag je M maar drie keer achter elkaar zetten. Het grootste getal wat je kan krijgen is dan MMMCMXCIX = 3999.

Toch grotere getallen?
Op Wikipedia staan wat manieren.

Binaire getallen

Het binaire getalsysteem is een tweetallig positiestelsel.
Als cijfers worden de tekens 0 en 1 gebruikt.
Zo'n cijfer wordt ook wel een bit genoemd.
Een binair getal met acht bits is een byte. Dus 8 b = 1 B.

De getallen 0 t/m 15:

Binair	Decimaal
0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	10
1011	11
1100	12
1101	13
1110	14
1111	15
10000	16

In het tientallig stelsel wordt 9 opgehoogd naar 10 en 99 opgehoogd naar 100. In het binaire systeem werkt het hetzelfde. Omdat je in het binaire stelsel alleen 0 en 1 hebt, wordt 1 direct opgehoogd naar 10 en 11 naar 100.

In het binaire systeem is de waarde van elk cijfer een macht van 2.
Vergelijk dit eventueel met de tabel voor het tientallig positiestelsel boven aan deze pagina.

	27	26	25	24	23	22	21	20
10011101	1	0	0	1	1	1	0	1

Het binaire getal 10011101 is in de decimale notatie:
2⁷ + 2⁴ + 2³ + 2² + 2⁰ = 128 + 16 + 8 + 4 + 1 = 157

Verwarring voorkomen

Om verwarring te voorkomen kan je met een subscript getal aangeven in welk getalsysteem een getal staat. In ons voorbeeld geldt dan: 10011101₂ = 157₁₀.

Octale getallen

Het octale getalsysteem is een achttallig positiestelsel.
Als cijfers worden de tekens 0 t/m 7 gebruikt.
Op de basisschool worden soms lessen aan het octale stelsel besteedt onder de naam: Het land van Oct of Het land van Okt.
In het land van Oct hebben mensen in totaal maar acht vingers en wordt dus met het achttallige systeem gewerkt. Het leert kinderen meer inzicht in de techniek achter het getalsysteem, je kunt immers niet meer op je geheugen vertrouwen maar moet echt rekenen. Om die reden kan de leerkracht sneller eventuele hiaten in het denkproces bij het (decimale) positiestelsel er mee opmerken.

De getallen 1₁₀ t/m 16₁₀ zijn in het octale stelsel:
1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20

10 wordt uitgesproken als oct, 11 als octéén, 12 als octtwee en 20 wordt uitgesproken als twee oct. Vanaf 100 hangt het af van de lesmethode. Meestal is 100 een bord (8×8) en 1000 een blok (8×8×8). Het getal 5342 wordt dus uitgesproken als vijf blok drie bord vier oct twee.

In het tientallig stelsel wordt 9 opgehoogd naar 10 en 99 opgehoogd naar 100. In het octale systeem werkt het hetzelfde. Een 7 wordt opgehoogd naar 10, 17 naar 20 en 77 naar 100.

Het octale getal 45 heeft als decimale waarde 4 × 8 + 5 = 37.
Het octale getal 371 heeft als decimale waarde 3 × 64 + 7 × 8 + 1 = 249.

In het octale systeem is de waarde van elk cijfer een macht van 8.
Vergelijk dit eventueel met de tabel voor het tientallig positiestelsel boven aan deze pagina.

	85	84	83	82	81	80
703 546	7	0	3	5	4	6

Het getal 703 546₈ is in de decimale notatie:
7 × 8⁵ + 0 × 8⁴ + 3 × 8³ + 5 × 8² + 4 × 8¹ + 6 × 8⁰ =
229 376 + 0 + 1536 + 320 + 32 + 6 = 231 270₁₀

Het land van Zeek

Er is ook een variant met een zestallig stelsel: het land van Zeek. Na 5 komt dan al 10 en dat noem je een 'zeek'. Na 55 komt dan 100 en dat noem je een 'azeka'. Het getal 352 wordt dus uitgesproken als drie azeka vijf zeek twee.

Babylonische getallen

Het Babylonische getalsysteem is het oudst bekende positiestelsel. Zij werkten met een zestigtallig (sexagesimaal) stelsel. Men had (gelukkig) geen 60 verschillende tekens maar gebruikte een additief systeem waarin 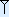voor 1 stond en 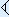voor 10. Deze tekens komen uit het spijkerschrift en worden spijkers en haken genoemd. Ze maakten deze met een hoekige stift in kleitabletten.
Zo is 23 in het zestigtallig stelsel .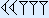

Men groepeert deze tekens bij meer dan drie. Zie hieronder 1 t/m 60.

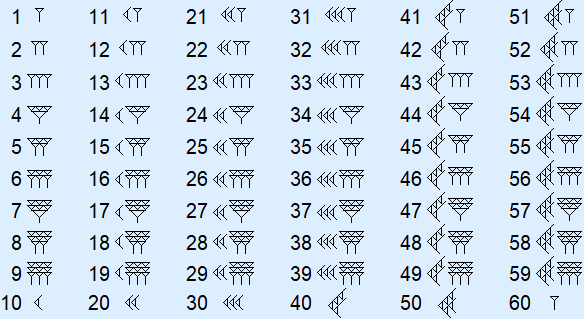
Zoals je kunt zien, zijn 1 en 60 hetzelfde. Dit komt omdat 60₁₀ in het zestigtallig stelsel eigenlijk het getal 10₆₀ is. Echter hadden de Babyloniërs geen teken voor nul. Zodoende werd alleen de 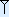opgeschreven met een (onzichtbare) spatie. 61 schrijf je daarom als twee spijkers met een spatie ertussen. Zie ook het laatste voorbeeld onder aan deze pagina.

Het getal 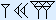heeft als decimale waarde 60 + 25 = 85.
Het getal 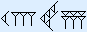heeft als decimale waarde 13 × 60 + 46 = 826.

In het sexagesimale systeem is de waarde van elk cijfer een macht van 60.

	603	602	601	600

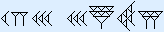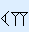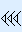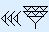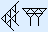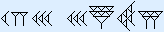heeft als decimale waarde:
12 × 60³ + 30 × 60² + 37 × 60¹ + 55 × 60⁰ = 
2 592 000 + 108 000 + 2220 + 55 = 2 702 275

Tijdwinst

Moet je veel Babylonische getallen schrijven?
Schrijf een haak gewoon als < en een spijker als |.
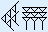wordt dan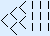

Handig?

Het ziet er uit als een zeer ingewikkeld systeem maar bedenk goed dat zij dit gewend waren zoals wij gewend zijn aan ons decimale systeem. Het feit dat hoeken verdeeld zijn in 360° en de tijd in 60 minuten en 60 seconden zijn nog overblijfselen van dit systeem. Ook zal je zien dat optellen en aftrekken onder elkaar in elk positiestelsel hetzelfde werkt.
Eén van de redenen dat voor 60 is gekozen is mogelijk omdat het getal zoveel delers heeft. Het heeft immers 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 en 60 als delers.

Optellen in de andere positiestelsels

Laten we eerst maar eens kijken hoe het ook al weer werkte in ons decimale positiestelsel. We nemen 30 728 + 42 744 en 174 213 + 894 892 als voorbeeld.

1 1 3 0  7 2 8 4 2  7 4 4 + 7 3  4 7 2

1 1 1 1  1 7 4  2 1 3  8 9 4  8 9 2 + 1  0 6 9  1 0 5

We kijken even naar het linkervoorbeeld. Omdat 8 + 4 = 12 schrijf je de 2 onder de streep en 'moet je 1 onthouden' en meenemen naar het volgende cijfer, in dit geval de tientallen. Deze schrijf je er klein boven (hier in het rood). Bij de honderdtallen krijg je 7 + 7 = 14. Je schrijft de 4 onder de streep en neemt de 1 mee naar de duizendtallen.

Binair optellen

Werkt precies hetzelfde. Omdat er maar twee cijfers zijn, zal je meestal vaker '1 moeten onthouden'.

1 1 1 0 1 0 1 0 0 1 1 1 0 0 1 1 0 0 1 + 1 1 1 0 1 1 0 0

1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 0 1 1 0 1 1 0 + 1 0 1 1 1 0 0 0 1

Octaal optellen

Werkt precies hetzelfde. Als je boven 7 uitkomt is de 'cijferpositie' vol, en zal je '1 moeten onthouden'.

1 1 1 5 3  7 4 0 7 2  5 6 4 + 1 4 6  5 2 4

1 1 1 2 1 7  6 0 3 3 6 7  1 3 5 + 6 0 6  7 4 0

We kijken even naar het linkervoorbeeld. Omdat 4 + 6 = 12 (octtwee) schrijf je de 2 onder de streep en 'moet je 1 onthouden' en dus meenemen. Je krijgt dan 1 + 7 + 5 = 15 (octvijf). Je schrijft de 5 onder de streep en neemt de 1 mee. In de laatste optelstap krijg je 5 + 7 = 14 (octvier).

Babylonisch optellen

Werkt volgens hetzelfde principe! Als je boven 9 spijkers uitkomt krijg je een extra haak en als je zes of meer haken hebt, laat je er zes weg en 'onthoud je een '.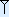

Voorbeeld 1

		+

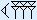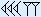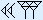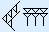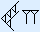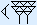Eerst tel je het aantal spijkers in de rechterkolom. Dat zijn er 2 + 6 = 8. Schrijf deze onder de streep. Nu ga je verder met de volgende kolom, die van de haken. Dat zijn er 3 + 4 = 7. Dit is er één meer dan 6, dus schrijf je één haak op onder de streep en telt een extra spijker mee in de volgende kolom.
Je krijgt in de volgende kolom in totaal 1 + 6 + 5 = 12 spijkers. Je schrijft 2 spijkers onder de streep en neemt een extra haak mee in de optelling van de haken. Je krijgt 1 + 1 + 2 = 4 haken.

Voorbeeld 2

			+

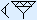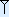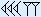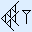Eerst tel je het aantal spijkers in de rechterkolom. Dat zijn er 4 + 7 = 11. Je zet één spijker neer en telt een extra haak mee in de volgende kolom. Zo krijg je 1 + 1 + 3 = 5 haken.
In de volgende kolom hebben we weer spijkers. Nu 7 + 5 = 12. Je zet twee spijkers neer en telt een extra haak mee in de volgende kolom. Zo krijg je 1 + 3 + 5 = 9 haken. Dit zijn er drie meer dan 6, dus schrijf je drie haken op onder de streep en telt een extra spijker mee in de volgende kolom. Hier wordt verder niets bij opgeteld, dus komt die ook zo onder de streep.

Voorbeeld 3: het gebrek aan een nul zorgt voor verwarring!

			+

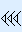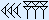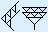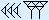Van rechts naar links in vogelvlucht:
9 + 6 = 15 dus 5 spijkers opschrijven en een haak meenemen.
1 + 5 + 3 = 9 dus 3 haken (meer dan 6) opschrijven en een spijker meenemen.
1 + 6 + 3 = 10 dus alleen een haak meenemen er is geen teken voor nul.
1 + 4 + 1 = 6 dus alleen een spijker meenemen er is geen teken voor nul.
1 + 6 + 0 = 7 dus 7 spijkers opschrijven.
1 + 3 = 4 dus 4 haken opschrijven.

Onze uitkomst  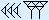    is verwarrend.
Wij bedoelen 47 × 60² + 0 × 60 + 35 × 1 = 169 235.
Echter door het ontbreken van de nul kan iemand ook denken dat hier bedoeld wordt: 47 × 60 + 35 × 1 = 2855.

De Babyloniërs vonden dit blijkbaar geen probleem en vanuit de context kon men meestal wel opmaken welke van de twee betekenissen bedoeld werd. Men gebruikte zelfs deze getallen tot achter de komma, maar gebruikten daar ook geen teken voor. Zo zijn er dus nog veel meer mogelijke interpretaties mogelijk van dit Babylonische getal.
Een 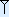kan dus worden geïnterpreteerd worden als ..., 3600, 60, 1, 1/60, 1/3600, ...
Op de stipjes kan je nog hogere machten van 60 invullen.

Plaatshouder

Later werd een 'plaatshouder' 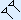voor een 'leeg' cijfer ingevoerd. Dit lost het probleem bij de uitkomst van voorbeeld 3 grotendeels op, daar het dan zo geschreven wordt:   

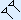
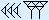
Zij gebruikten dit teken echter niet aan het einde van het getal. Een enkele spijker kon dus nog steeds 3600, 60, 1, et cetera zijn. Deze plaatshouder is dus nog steeds geen 'echte' nul.

Dus wees dankbaar voor onze nul en komma!

Naar boven