Trigonometry » Law of sines
Note: The length a and the angle size α (alpha) are used both, look closely at the difference between the two letters.
Contents
What is the law of sines?How do you calculate with the law of sines?
Proof of the law of sines
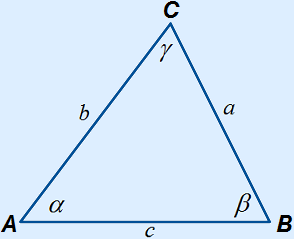
What is the law of sines?
The law of sines is for triangle ABC in which α = 
A, β = B, γ = C, a = BC, b = AC and c = AB is:
asin(α) = bsin(β) = csin(γ)
With just normal letters:
BCsin(A) = ACsin(B) = ABsin(C)
How do you calculate with the law of sines?
The easiest way is using a ratio table.
You fill in the table like this:
| a | b | c |
sin(α) |
sin(β) |
sin(γ) |
Then you use cross multiplication to calculate the unknown sides and/or angles.
Example
Given is the following triangle.
Calculate the unknown angles and side.
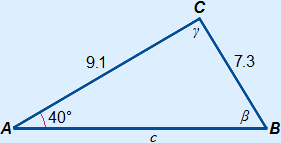
Fill in the table:
| 7.3 | 9.1 | c |
sin(40°) |
sin(β) |
sin(γ) |
First calculate β.
sin(β) = 9.1 × sin(40°)7.3 = 0.801...
β = sin–1(0.801...) = 53.253...°
As the sum of the angles in a triangle is 180°, you can calculate the third angle.
γ = 180° – α – β = 180° – 40 – 53.253...° = 86.747...°
With this new data, the table will look like this:
| 7.3 | 9.1 | c |
sin(40°) |
sin(53.253...°) |
sin(86.747...°) |
Now we can calculate side c:
c = 7.3 × sin(86.747...°)sin(40°) ≈ 11.3
Proof of the law of sines
To prove the law of sines, we use an altitude.
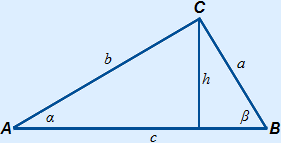
The following is now true:
sin(α) = hb and sin(β) = ha
Rearranging gives:
h = b · sin(α) and h = a · sin(β)
This gives:
a · sin(β) = b · sin(α)
Rearranging gives:
asin(α) = bsin(β)