Trigonometry » Tangent

The following formula is for the tangent:
tan(A) = opposite shorter side of Aadjacent shorter side of A

Check opposite and adjacent side if you need more information about this.

How do you use the tangent?

Use the following plan/steps/method:

1. Draw a sketch if it is not yet given.
2. Write down the rule: tan(...) = oa.
3. Fill in the data that is given.
4. Calculate the unknown value. If necessary, use  2 = 63.

Example 1: Calculate an angle

Question: Calculate A, round your answer to one decimal. Answer: 2. tan(A) = oa 3. tan(A) = 103 4. A = tan-1(103) ≈ 73.3°

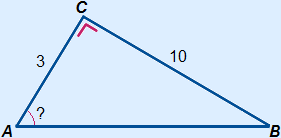Note to step 4:
- On your calculator, you do: [2nd] or [shift] tan (10 : 3) ≈ 73.301
- Sometimes arctan has to be used instead of tan^-1.

Example 2: Calculate a side

Question:
Given is triangle ABC with B = 20°, C = 90° and BC = 10 m.
Calculate the length of AC, round your answer to one decimal.

Answer:

1.	Draw a sketch first.

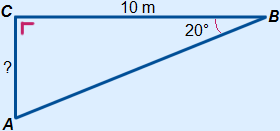2. tan(B) = oa

3. tan(20°) = ?10

4.	Use 2 = 63
	The ? is at the location of the 6. To get 6, you have to do 2 × 3. Looking back to step 3, we have to do tan(20°) × 10. AC = tan(20°) × 10 ≈ 3.6 m

Note to step 4:

-	You do not have to key in the °-sign on the calculator.
-	Some calculators do not automatically put a '(' behind tan. If you want you can just key in tan 20 × 10.

Example 3: Calculate a side

Question:
Given is triangle ABC with A = 68°, C = 90° and BC = 8.5 m.
Calculate the length of AC, round your answer to one decimal.

Answer:

1.	Draw a sketch first.

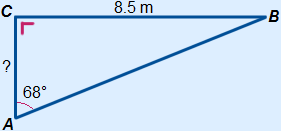2. tan(A) = oa

3. tan(68°) = 8.5?

4.	Use 2 = 63
	The ? is at the location of the 3. To get 3, you have to do 6 : 2. Looking back to step 3, we have to do 8.5 : tan(68°). AC = 8.5 : tan(68°) ≈ 3.4 m

Note to step 4:

-	You do not have to key in the °-sign on the calculator.
-	Some calculators do not automatically put a '(' behind tan. If you want you can just key in 8.5 : tan 68.