Differentiation and integration » Optimization

In optimization problems you are asked for the maximum or minimum value of a given variable. For example, you may be asked about the maximum size of the contents of a box or the minimum cost of the fences of a plot.

When solving algebraic optimization problems, follow the schedule underneath:
1. Deduce from the question which two variables play a role.
2. Make a formula for both variables.
3. Rearrange the formula of the variable which is not asked.
4. Substitute the rearranged formula in the other.
5. Differentiate and solve the equation to zero. Because in the maximum or minimum the gradient is zero.
6. The found value must sometimes be filled in the other formula to find the other dimension or to calculate the minimum cost.

Example 1
A farmer wants a rectangular piece of land fenced with barbed wire. He also wants this piece of land divided into 4 equal pieces. See the drawing below.
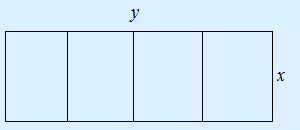
   drawing with total width being four pieces together measuring y and height x
The farmer has a roll of barbed wire with a length of 360 metres. With which measurements will he get the maximum area?

Solution
1. The variables here are the length of the barbed wire and the area.
2. length = 2y + 5x and area = xy.
3. The length of the barbed wire is 360 metres.
The formula will become: 360 = 2y + 5x.
When you rearrange the formula to express x in terms of y you will get:
x = –0,4y + 72  (you subtract 2y and divide by 5)
4. When you substitute x in the other formula by this expression you will get:
area = (–0,4y + 72)y
Removing the brackets will give you: –0,4y2 + 72y.
5. In order to calculate the dimensions, where you will have the maximum area, this formula is to be differentiated and solved to zero:
     –0.8y + 72 = 0
–0.8y = –72
y = 90 metres
6. In order to calculate the x-value we fill in the y-value in the formula for the length:
     360 = 2 × 90 + 5x
360 = 180 + 5x
5x = 180
x = 36 metres

Example 2
A farmer is fencing off a rectangular piece of land. He also wants this land divided into 4 equal pieces. The fence at the edges of his land he uses a fence of 20 euros per metre. The other pieces cost 10 euros per metre fence. See the drawing below.
   drawing with total width being four pieces together measuring y and height x
The farmer wants a pice of land measuring 480 square metres. With wich measurements can he minimalize his costs?

Solution
1. The variables are area and costs.
2. area = xy and costs = 20y + 20y + 20x + 20x + 10x + 10x + 10x = 40y + 70x.
3. The area is 480 metres, filling this in will give you: 480 = xy. Rearranging gives you: x = 480y .
4. Substituting this formula for x gives you:
costs = 40y + 70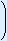haakje openen480yhaakje openen = 40y + 33600y = 40y + 33600y–1
5. To calculate for which value the costs are minimum we differentiate and solve the differentiated formula to zero:
  40 – 33600y2 = 0
33600y2 = 40
y2 = 840 
y ≈ 29,0
6. If you fill in this y-value in the formula of the area, the x-value can be calculated.
x = 48029.0 ≈ 16.6 metres.