Differentiëren en integreren » Optimaliseren

Bij optimaliseringsproblemen wordt er gevraagd naar de maximale of minimale waarde van een bepaalde grootheid. Er kan bijvoorbeeld worden gevraagd naar de maximale afmetingen van de inhoud van een doos of de minimale kosten van de omheinig van een stuk land.

Bij het algebraïsch oplossen van optimaliseringsproblemen kan het volgende schema worden gevolgd:

1.	Leid uit de situatie af welke twee grootheden een rol spelen. (In de vraagstelling staat één van deze grootheden.)
2.	Stel van beide grootheden de formule op.
3.	Maak uit de formule van de grootheid, die niet gevraagd wordt, één van de variabelen vrij.
4.	Substitueer de gevonden uitdrukking in de formule van de grootheid, die wel gevraagd wordt.
5.	Differentieer en stel gelijk aan nul. In het maximum of minimum is de helling immers nul.
6.	De gevonden waarde moet soms in de gewone formule worden ingevuld om de andere afmeting of de minimale kosten te berekenen.

Voorbeeld 1
Boer Hans wil een rechthoekig stuk land afzetten met prikkeldraad. Daarnaast wil hij dit stuk land verdelen in 4 even grote stukken. Zie de onderstaande tekening.
   
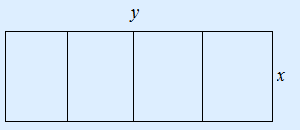
Hans heeft een rol prikkeldraad met een lengte van 360 meter. Bij welke afmetingen is het oppervlak maximaal.

Uitwerking

1.	De lengte van het prikkeldraad en de oppervlakte spelen een rol.
2.	lengte = 2y + 5x en oppervlakte = xy.
3.	De lengte van het prikkeldraad wordt niet gevraagd en is al gegeven, namelijk 360 meter. De formule wordt dan: 360 = 2y + 5x. Als x wordt vrijgemaakt, dan krijg je: x = –0,4y + 72. (2y naar de andere kant brengen en delen door 5).
4.	Als deze uitdrukking voor x wordt ingevuld in de formule van de oppervlakte, dan krijg je: oppervlakte = (–0,4y + 72)y. En na het wegwerken van de haakjes: –0,4y2 + 72y.
5.	Om de afmetingen met de maximale oppervlakte te berekenen, moet deze formule gedifferentieerd worden en gelijk worden gesteld aan nul:      –0,8y + 72  = 0 –0,8y  = –72 y  = 90 meter
6.	Nu kan je met deze y-waarde in de formule x = –0,4y + 72 de x-waarde berekenen: x = –0,4 × 90 + 72 = 36 meter.

Voorbeeld 2
Boer Henk wil een rechthoekig stuk land afzetten met een hek. Daarnaast wil hij dit stuk land verdelen in 4 even grote stukken. Voor het hek aan de rand van zijn land gebruikt hij een hek van 20 euro per meter. De overige stukken hek kosten 10 euro per meter. Zie de onderstaande tekening.
   
Hans wil een stuk land van 480 vierkante meter afzetten. Bij welke afmetingen zijn de kosten minimaal.

Uitwerking

1.	De oppervlakte en de kosten spelen een rol.
2.	oppervlakte = xy kosten = 20y + 20y + 20x + 20x + 10x + 10x + 10x = 40y + 70x.
3.	De oppervlakte wordt niet gevraagd en is al gegeven, namelijk 480 vierkante meter. De formule wordt dan: 480 = xy. Herschrijven geeft: x = 480y.
4.	Vul deze uitdrukking voor x in, in de formule van de kosten, je krijgt: kosten = 40y + 70480y = 40y + 33600y = 40y + 33600y–1
5.	Om de afmetingen te berekenen, waarbij de kosten minimaal zijn, dient deze formule gedifferentieerd te worden en gelijk worden gesteld aan nul:   40 – 33600y2  = 0 33600y2  = 40 y2  = 840  y  ≈ 29,0
6.	Als deze y-waarde in de formule van de oppervlakte wordt ingevuld, kan de x-waarde worden berekend. x = 48029,0 ≈ 16,6 meter.