Differentiëren en integreren » Primitieve functies
Regels:
| Functie f (x) | Primitieve functie F (x) |
| axn | an + 1xn + 1 + c (n ≠ –1) |
| 1x = x–1 | ln|x| + c |
| ex | ex + c |
| eax + b | 1aeax + b + c |
| gx | gxln(g) + c |
| gax + b | 1a · gax + bln(g) + c |
ln(x) |
x ln(x) – x + c |
glog(x) = ln(x)ln(g) |
1ln(g)(x ln(x) – x) + c |
sin(ax + b) |
–1acos(ax + b) + c |
cos(ax + b) |
1asin(ax + b) + c |
sin2(ax) = 12 – 12cos(2ax) |
12x – 14asin(2ax) + c |
cos2(ax) = 12 + 12cos(2ax) |
12x + 14asin(2ax) + c |
tan2(x) = 1 + tan2(x) – 1 |
tan(x) – x + c |
Voorbeelden:
| f (x) | F (x) | |||
| 5x | 52x2 + c = 212x2 + c | |||
10x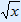 = 10x1,5 = 10x1,5 |
102,5x2,5 + c = 4x2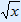 + c + c |
|||
| x6 + 2x2 – 7x2 = x4 + 2 – 7x–2 | 15x5 + 2x + 7x–1 + c = 15x5 + 2x + 7x + c | |||
| e3x + 2 + 25x | 13e3x + 2 + 15 · 25xln(2) + c = 13e3x + 2 + 25x5 ln(2) + c |
|||
|
x + 1ln(3)(x ln(x) – x) + c |
|||
3sin(2x – 13π) |
–32cos(2x – 13π) + c |
|||
1 – 5cos(12(x + 14π)) |
x – 10sin(12(x + 14π)) + c |
|||
4sin2(32x) = 2 – 2cos(3x) |
2x – 23sin(3x) + c |
|||
cos2(4x) = 12 + 12cos(8x) |
12x + 116sin(8x) + c |