Equations » Logarithmic equations
ln(x) = elog(x) with e = 2.71828182846...
Check logarithm rules if needed too.
Example 1
3log(x – 2) | = 1 + 4 · 3log(2) |
3log(x – 2) | = 3log(3) + 3log(24) |
3log(x – 2) | = 3log(3) + 3log(16) |
3log(x – 2) | = 3log(3 · 16) |
3log(x – 2) | = 3log(48) |
| x – 2 | = 48 |
| x | = 50 |
Example 2
1 + 2 · 2log(x) | = 2log(5x + 3) |
2log(2) + 2log(x2) | = 2log(5x + 3) |
2log(2x2) | = 2log(5x + 3) |
| 2x2 | = 5x + 3 |
| 2x2 – 5x – 3 | = 0 |
| D = (–5)2 – 4 · 2 · –3 = 49 | |
x = –(–5) + 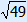 2 · 2 2 · 2 | or x = –(–5) – 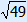 2 · 2 2 · 2 |
| x = 3 | or x = –12 |
Example 3
0.5log(x + 6) + 2 · 2log(x) | = 0 |
–2log(x + 6) + 2log(x2) | = 0 |
–2log(x + 6) | = –2log(x2) |
| x + 6 | = x2 |
| –x2 + x + 6 | = 0 |
| x2 – x – 6 | = 0 |
| (x + 2)(x – 3) | = 0 |
| x = –2 or x = | 3 |
As x = –2 is not a solution to the original equation, the correct solution is only x = 3.
Example 4
(3log(x) )2 – 3log(x) = 0
Substitute: p = 3log(x)
| p2 – | p = 0 |
| p(p – | 1) = 0 |
| p = 0 | or p = 1 |
3log(x) = 0 | or 3log(x) = 1 |
| x = 1 | or x = 3 |
Example 5
4log(x) | = 2log(x – 2) |
2log(x)2log(4) | = 2log(x – 2) |
2log(x)2 | = 2log(x – 2) |
2log(x) | = 2 · 2log(x – 2) |
2log(x) | = 2log( (x – 2)2 ) |
| x | = (x – 2)2 |
| x | = (x – 2)(x – 2) |
| x | = x2 – 4x + 4 |
| 0 | = x2 – 5x + 4 |
| 0 | = (x – 1)(x – 4) |
| x = 1 or x = 4 |
As x = 1 is not a solution to the original equation, the correct solution is only x = 4.