Equations » Square root equations
To solve square root equations follow these steps:
| 1. | Isolate the square root; so put the root form separate or use substitution as in example 3. |
| 2. | Square the left-hand side and the right-hand side of the equation. |
| 3. | Check whether the solutions of the squared equation are also solutions of the original equation. |
Example 1
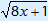 | = 3x |
(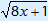 )2 )2 | = (3x)2 |
| 8x + 1 | = 9x2 |
| –9x2 + 8x + 1 | = 0 |
| D = 82 – 4 · –9 · 1 = 100 | |
x = –8 + 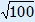 2 · –9 2 · –9 | or x = –8 – 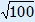 2 · –9 2 · –9 |
| x = –19 | or x = 1 |
Check:
Only x = 1 is a good solution when filling it in into the original equation.
Example 2
2x – 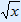 | = 10 |
| 2x – 10 | = 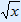 |
| (2x – 10)2 | = (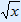 )2 )2 |
| 4x2 – 40x + 100 | = x |
| 4x2 – 41x + 100 | = 0 |
| D = (–41)2 – 4 · 4 · –100 = 81 | |
x = –(–41) + 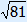 2 · 4 2 · 4 | or x = –(–41) – 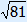 2 · 4 2 · 4 |
| x = 614 | or x = 4 |
Check:
Only x = 614 is a good solution when filling it in into the original equation.
Example 3
x5 – x2 · 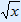 | = 2 |
x5 – x2 · 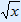 – 2 – 2 | = 0 |
| x5 – x2 · x0.5 – 2 | = 0 |
| x5 – x2.5 – 2 | = 0 |
| Substitute: p = x2.5 | |
| p2 – p – 2 | = 0 |
| (p + 1)(p – 2) | = 0 |
| p = –1 | or p = 2 |
| x2.5 = –1 | or x2.5 = 2 |
| x = (–1)12.5 | or x = 212.5 |
| x = –1 | or x ≈ 1.32 |
Check:
Only the solution x ≈ 1.32 is correct when used in the original equation.
Do you want an exact solution instead of x ≈ 1.32?
| x2.5 | = 2 |
| (x2.5)2 | = 22 |
| x5 | = 4 |
| x | = 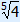 |