Geometry » Special lines
Contents
1. Angle bisector2. Perpendicular bisector
3. Median
4. Altitude
5. Mid-parallel
1. Angle bisector
The angle bisector divides an angle into two equal parts.
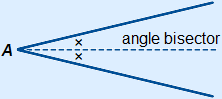
To construct an angle bisector you need a pair of compasses and a ruler.
Click here to show how this is done.
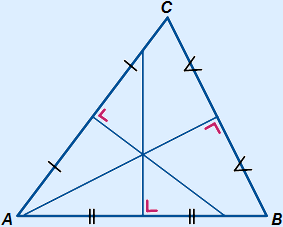
The three angle bisectors in a triangle will intersect in one point. This is shown in the picture on the left.
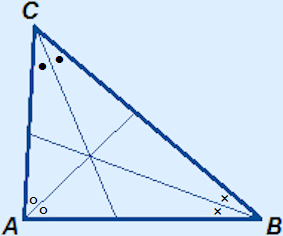
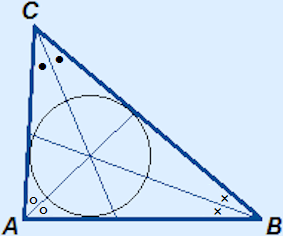
Incircle
If you would draw a circle with centre S and radius the shortest distance from S to one of the sides, you will get the incircle of the triangle.
See this in GeoGebra!
2. Perpendicular bisector
The perpendicular bisector between two points is a line segment that intersects the line segment between those two points in the middle at an angle of 90 °.
Below you can see the perpendicular bisector of line segment AB.
Every point on the perpendicular bisector is equidistant to A and B.
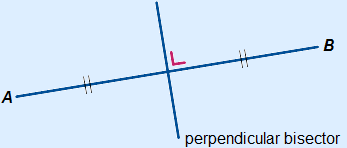
To construct a perpendicular bisector you need a pair of compasses and a ruler.
Click here to show how this is done.
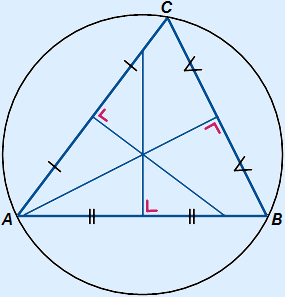
The three perpendicular bisectors of a triangle will intersect in one point. This is shown in the picture on the left.
In case of an obtuse-angled triangle this intersection will be outside the triangle!
 |
|
Circumcircle
You can use the intersection of the perpendicular bisectors to draw the circumcircle.
See this in GeoGebra! You can also see what happens with an obtuse-angled triangle.
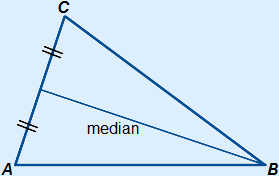
3. Median
The median of a triangle is a line through one of the vertices of the triangle to the middle of the opposite side of this vertex.
The area on both sides of the median is equal. For that reason the weight of the triangle on both sides is also equal, therefore you can balance the triangle on that line. Small technicality: when a triangle has weight you actually have a prism.
Centroid
The three medians in a triangle will intersect in one point.
This point is called the centroid.
The centroid is the centre of gravity of the triangle.
For that reason you can balance the triangle on a sharp tip by putting the triangle with its centroid exactly on the sharp tip.
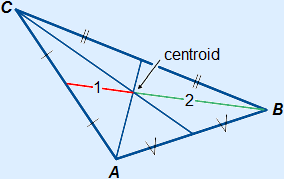
The medians intersect each other with a ratio of 1 : 2.
In the figure above, the red part is always half as long as the green part of the median starting in point B.
See this in GeoGebra!
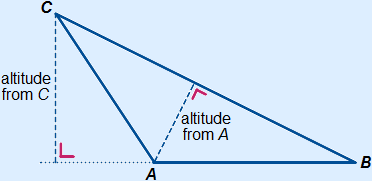
4. Altitude
An altitude is the shortest distance between a certain point and a line. The shortest distance is always perpendicular to the line. Sometimes the altitude is called the perpendicular.
Below you can see two altitudes.
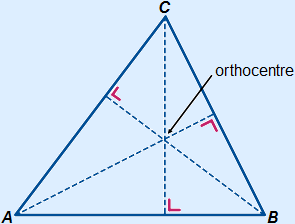
Orthocentre
The three altitudes in a triangle will intersect in one point.
This point is called the orthocentre.
In case of an obtuse-angled triangle, the orthocentre will be outside of the triangle.
See this in GeoGebra!
You can also see what happens with an obtuse-angled triangle.
5. Mid-parallel
A line that connects the middle of one side with the middle of another side in a triangle is called a mid-parallel. Every mid-parallel is parallel to one of the sides in the triangle and is half the size of the side it runs parallel with.
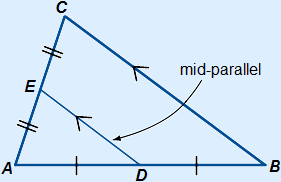
In the figure above DE is parallel to BC and DE is half as long as BC.
See this in GeoGebra!