Herleiden » Haakjes wegwerken

In een formule staan soms haakjes. Deze haakjes kun je wegwerken.
Als een formule herleid moet worden, moeten altijd de haakjes weg gewerkt worden.

Het wegwerken van haakjes kan op drie manieren:
1. Rechthoekmethode
2. Papegaaienbekmethode
3. Vermenigvuldigtabel

Methode 1 levert tevens het bewijs dat beide formules gelijk zijn.

Handig is uiteraard om te weten dat de keer weggelaten mag worden.
Dus 5a betekent 5 × a en 4(3 + a) betekent 4 × (3 + a)

Inhoud

Enkele haakjes
    1. Rechthoekmethode
    2. Papegaaienbekmethode
    3. Vermenigvuldigtabel
    4. Voorbeelden enkele haakjes
Dubbele haakjes
    1. Rechthoekmethode
    2. Papegaaienbekmethode
    3. Vermenigvuldigtabel
    4. Voorbeelden dubbele haakjes

Enkele haakjes

Methode 1: Rechthoekmethode

Stel je wilt de formule q = 2(p + 8) zonder haakjes schrijven.
Dan kun je dat doen door je een rechthoek voor te stellen met een hoogte van 2 en een breedte van p + 8.
rechthoek met hoogte 2 en breedte p + 8
De oppervlakte van deze rechthoek is 2 × p + 2 × 8 = 2p + 16. Dus:
q = 2(p + 8) = 2p + 16.

Je kan ook zien dat in de rechthoek het linkervakje een oppervlakte heeft van 2p en het rechtervakje van 2 × 8 = 16. Samen q = 2p+ 16.

Methode 2: Papegaaienbekmethode

De papagaaienbekmethode is de snelste van alle drie. Je weet dat je de factor die voor (of achter) de haakjes staat, moet vermenigvuldigen met de termen tussen de haakjes. Als hulp kan je pijlen (of lijen) tekenen van de factor naar de termen. Langs die pijlen ga je dan vermenigvuldigen. Als je dit eenmaal doorhebt, dan hoef je de pijlen niet meer te tekenen.
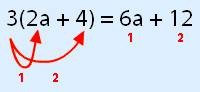
3(2a + 4) = 6a + 12 met pijlen
Pijl 1 geeft 3 × 2a = 6a
Pijl 2 geeft 3 × 4 = 12

Methode 3: Vermenigvuldigtabel

De opgave zet je met deze methode in een vermenigvuldigtabel.
De factor komt in de eerste kolom te staan en de termen in de bovenste rij.
Dan ga je de factor vermenigvuldigen met de termen.

Voorbeeld
Herleid b = 5a(2a + 4)

×	2`a`	4
5`a`	10`a`²	20`a`

De groene tekst vul je in aan de hand van de gegeven formule. Het rode reken je uit.
Het antwoord is dan de rode vakjes opgeteld.
In dit geval dus b = 10a² + 20a

Voorbeelden enkele haakjes

b = 3a(5a + 3) = 15a² + 9a
b = 3a(5a – 3) = 15a² – 9a
b = 3a(–5a + 3) = –15a² + 9a
b = 3a(–5a – 3) = –15a² – 9a
b = –3a(5a + 3) = –15a² – 9a
b = –3a(5a – 3) = –15a² + 9a
b = –3a(–5a + 3) = 15a² – 9a
b = –3a(–5a – 3) = 15a² + 9a

Let op:
b = –(5a – 3) = –5a + 3
b = (4a – 7)3 = 12a – 21
b = (4a – 7) + 3 = 4a – 7 + 3 = 4a – 4

Voorbeeld voor gevorderden (tussenstappen staan onder elkaar):
–2a(b – 3c) – 5c(a + 2b) =
–2ab + 6ac – (5ac + 10bc) =
–2ab + 6ac – 5ac – 10bc =
–2ab + ac – 10bc

Dubbele haakjes

Methode 1: Rechthoekmethode

Stel je wilt de formule q = (p + 3)(p + 8) zonder haakjes schrijven.
Dan kun je dat doen door je een rechthoek voor te stellen met een hoogte van p + 3 en een breedte van p + 8.
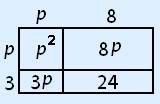
rechthoek met hoogte p + 3 en breedte p + 8
Je kan van ieder vakje de oppervlakte berekenen
De oppervlakte van de hele rechthoek is dan:
q = p² + 8p + 3p + 24 = p² + 11p + 24.

Methode 2: Papegaaienbekmethode

De papagaaienbekmethode is weer de snelste van alle drie. Je zorgt dat je iedere term tussen de eerste haakjes een keer vermenigvuldigt met elke termen tussen de tweede haakjes.
Als hulp kan je weer de pijlen (of lijnen) tekenen. Langs die pijlen ga je dan vermenigvuldigen.
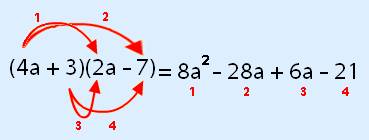
(4a + 3)(2a - 7) = 8a^2 - 28a + 6a -21 met pijlen
Pijl 1 geeft 4a × 2a = 8a²
Pijl 2 geeft 4a × –7 = –28a
Pijl 3 geeft 3 × 2a = 6a
Pijl 4 geeft 3 × –7 = –21
Deze tel je alle vier op en dan krijg je:
8a² – 28a + 6a – 21 = 8a² – 22a – 21

Methode 3: Vermenigvuldigtabel

De opgave zet je met deze methode in een vermenigvuldigtabel.
De twee termen van de eerste factor komen onder elkaar in de eerste kolom te staan
en de termen van de tweede factor naast elkaar in de bovenste rij.

Voorbeeld
Herleid b = (3 + 5a)(2a – 4)

×	2`a`	–4
3	6`a`	–12
5`a`	10`a`²	–20`a`

De groene tekst vul je in aan de hand van de gegeven formule. Het rode reken je uit.
Het antwoord is dan de rode vakjes opgeteld.
In dit geval dus b = 6a + –12 + 10a² + –20a = 10a² – 14a – 12.

Voorbeelden dubbele haakjes

(2`a` + 3)(4`a` + 3) = 8`a`² + 6`a` + 12`a` + 9 = 8`a`² + 18`a` + 9	(3`a` + 2)(5`a` – 3) = 15`a`² – 9`a` + 10`a` – 6 15`a`² + `a` – 6

(5`a` – 7)(4`a` – 6) = 20`a`² – 30`a` – 28`a` + 42 = 20`a`² – 58`a` + 42	(5`a` + 3`b`)(2`a` – 7`b`) = 10`a`² – 35`ab` + 6`ab` – 21`b`² = 10`a`² – 29`ab` – 21`b`²

–(2`a` + 4)(5`a` – 3) = –(10`a`² – 6`a` + 20`a` – 12 = –(10`a`² + 14`a` – 12) = –10`a`² – 14`a` + 12	5(3`a` + 5)(2`a` + 3) = 5(6`a`² + 9`a` + 10`a` + 15) = 5(6`a`² + 19`a` + 15) = 30`a`² + 95`a` + 75

(3`a` – 4`a`²)(5`a` – 3) = 15`a`² – 9`a` – 20`a`³ + 12`a`² = –20`a`³ + 27`a`² – 9`a`	(3`a`²`b` – `b`³)(2`b`² – `a`) = 6`a`²`b`³ – 3`a`³`b` – 2`b`⁵ + `ab`³

Naar boven