Kansrekening » Vaasmodel
Voorkennis:
De theorie over kansen en combinaties.
Wat is het vaasmodel?
Het vaasmodel kan alleen gebruikt worden als er sprake is van 'zonder terugleggen'. Zonder terugleggen houdt in dat de kansen niet hetzelfde blijven. Dit kan als volgt duidelijk worden gemaakt.
Voorbeeld 1
Stel ik heb de volgende vaas met 4 rode en 6 blauwe knikkers.
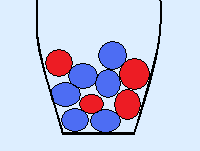
Ik pak er 2 keer achter elkaar een knikker uit zonder deze terug te leggen.
De kans om de eerste keer een rode knikker te pakken is 410.
Er zijn in totaal 10 knikkers, waarvan er 4 rood zijn.
Maar bij de tweede keer is de kans niet meer 410.
Er zijn nu in totaal 9 knikkers, waarvan er 3 rood zijn. De kans is dus 39.
De kans op twee rode knikkers is dan 410 × 39 = 215.
Dezelfde kans is te berekenen met combinaties.
Volgens de kansdefinitie moeten we het aantal gunstige uitkomsten delen door het totaal aantal uitkomsten.
Het makkelijkst is om te beginnen met het totaal aantal uitkomsten.
Het totaal aantal uitkomsten kan berekend worden met 10 nCr 2. Van de 10 knikkers pak je er 2.
Vervolgens kunnen de gunstige uitkomsten berekend worden.
Het aantal combinaties om 2 rode knikkers te pakken uit 4 rode knikkers is 4 nCr 2.
Dit moet nog vermenigvuldigd worden met het aantal manieren om 0 blauwe knikkers uit 6 blauwe knikkers te pakken. Dit is 6 nCr 0.
Uiteindelijk krijg je de volgende berekening:
Kans = aantal gunstige uitkomstenaantal mogelijke uitkomsten = 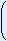 4
4
2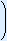
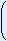 6
6
0
 10
10
2 = 6 · 145 = 215
= 6 · 145 = 215
Deze berekening met combinaties lijkt bij dit voorbeeld erg omslachtig, maar bij grotere aantallen is dit zeer handig.
Voorbeeld 2
In dit voorbeeld zal het nut van het vaasmodel getoond worden bij een loterij.
Stel er is een loterij met 20 loten.
Er is 1 hoofdprijs van 10 euro.
Er zijn 3 tweede prijzen van 5 euro.
Ik heb 3 loten in de loterij gekocht.
Bereken de kans dat je precies 10 euro wint.
Antwoord:
De loterij kan als volgt worden voorgesteld.
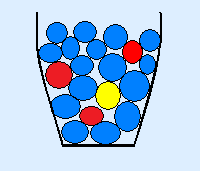
Er zijn 20 loten. Dit zijn dan in totaal 20 knikkers in de vaas.
Er is 1 hoofdprijs. Dit is de gele knikker in de vaas.
Er zijn 3 tweede prijzen. Dit zijn de 3 rode knikkers in de vaas.
Op de rest van de loten valt geen prijs. Dit zijn er 16 en deze zijn blauw.
Er zijn twee mogelijkheden om 10 euro te winnen:
1. Ik win de hoofdprijs en verder niks.
2. Ik win 2 tweede prijzen en verder niks.
Beide kansen moet ik bij elkaar optellen.
Kans = 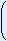 1
1
1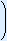
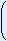 16
16
2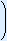
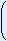 20
20
3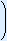 +
+
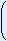 3
3
2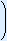
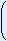 16
16
1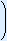
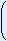 20
20
3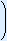 =
1 · 1201140 + 3 · 161140 = 1681140 = 1495
=
1 · 1201140 + 3 · 161140 = 1681140 = 1495