Probabilities » Binomial distribution

Contents

1. Bernoulli trial
2. Binomial probability experiment
3. Binomial distribution on the graphical calculator
4. Converting binomial probabilities

1. Bernoulli trial

A random experiment with only two outcomes is Bernoulli trial. Throwing a coin is a good example; there are only two possible outcomes. However, throwing a die can also be a Bernoulli trial. Let's say you want to throw a six. The outcome will be a six or not a six. Therefore every yes or no question can serve as a Bernoulli trial.
In a Bernoulli trial you often talk about success and failure.
The probability of a good outcome often is called p.

Examples

-	Do you get heads when flipping a coin?
-	Is a newborn a girl?
-	Does someone vote for the party leader?
-	Do you have the correct answer for a multiple choice question?

2. Binomial probability experiment

A probability experiment that consists of a Bernoulli trials that is repeated a number of times is a binomial probability experiment. The number of times you repeat the trial is called n. The probability of a good outcome per trial is called p. The coincidence variable X is the number of times success happens in the probability experiment. X is called a binomial coincidence variable in this case. X is distributed binomially.

Examples

Binomial probability experiment	n	p
throwing a die 15 times X = the number of times a six is thrown	15	16
taking a marble 25 times with replacing from a vase with five blue and four red marbles X = the number of times a blue marble is taken	25	59
Guessing a four-choice question 30 times X = the number of times correct	30	14

We use the last example to show how to calculate this probability. We are going to calculate P(X = 10). We will have to get a sequence with 10 times success and 20 times failure. The probability for success is 14 and the probability for failure is 34.
This sequence can be written in  30
10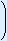 different orders.

Therefore, the probability can be calculated with:
P(X = 10) = 30
10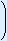 · (14)¹⁰ · (34)²⁰

From this you can derive the general rule.

With a binomial probability experiment, the probability for k times success is:
P(X = k) = n
k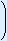 · p^k · (1 – p)^(n – k)

3. Binomial distribution on the graphical calculator

The graphical calculator can do these calculations a lot quicker with the options binompdf en binomcdf, the c in binomcdf stands for cumulative.
Here is:
P(X = k) = binompdf(n, p, k)
P(X ≤ k) = binomcdf(n, p, k)

On a Casio you have to use BinominalPD(k, n, p) and BinominalCD(k, n, p).

Example 1
Throwing exactly two times 3 spots when throwing a die 8 times.
Answer: P(X = 2) = binompdf(8, 1/6, 2) ≈ 0.260

Example 2
Throwing at most three times 6 spots when throwing a die 10 times.
Note: You may throw 0, 1, 2 or 3 times 6 spots.
Answer: P(X ≤ 3) = binomcdf(10, 1/6, 3) ≈ 0.930

4. Converting binomial probabilities

On the graphical calculator you only have binompdf and binomcdf. Sometimes you will need to calculate a different probability than 'equal to' or 'at most'.
Below you can find a couple of examples showing how you can calculate those.

P(5 or 6 successes) = P(X = 5) + P(X = 6)
P(less than 5 successes) = P(X < 5) = P(X ≤ 4)
P(more than 5 successes) = P(X > 5) = 1 – P(X ≤ 5)
P(at least 5 successes) = P(X ≥ 5) = 1 – P(X ≤ 4)
P(between 5 and 8 successes) = P(5 < X < 8) = P(X ≤ 7) – P(X ≤ 5)
P(between or equal to 5 and 8 successes) = P(5 ≤ X ≤ 8) = P(X ≤ 8) – P(X ≤ 4)

Example
For a binomial probability experiment with n = 15 and p = 0.4 is X the number of times success.
P(X < 9) = P(X ≤ 8) = binomcdf(15, 0.4, 8) ≈ 0.905
P(X > 8) = 1 – P(X ≤ 8) = 1 – binomcdf(15, 0.4, 8) ≈ 0.095
P(X ≥ 6) = 1 – P(X ≤ 5) = 1 – binomcdf(15, 0.4, 5) ≈ 0.597
P(6 < X < 12) = P(X ≤ 11) – P(X ≤ 6) = binomcdf(15, 0.4, 11) – binomcdf(15, 0.4, 6) ≈ 0.388

To top