Probability » Coincidence variables

According to the probability definition of Laplace (check probabilities) probabilities are defined by the number of good outcomes divided by the number of possible outcomes. Often, the good outcomes are not written in full, but a variable is used. This variable can have different values, so different events can all be written in a short way.

The coincidence variable is also called a random variable or a stochastic variable.

Example 1
X = the number of pips on a regular 6-faced dice

1) P(X = 1) means the probability the number of pips thrown is 1.
2) P(X < 4) means the probability the number of pips thrown is less than 4.
3) P(X > 4) means the probability the number of pips thrown is greater than 3.

The answers:
1) P(X = 1) = 16
2) P(X < 4) = 12
3) P(X > 4) = 13

Example 2
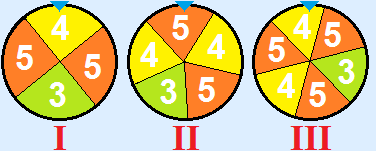
three spinning tops, first has one 3, one 4 and two 5's. Second has one 3, two 4's and two 5's. Third has one 3, two 4's and three 5's.
X = is the sum of the three numbers spinned

1) P(X = 8) means the probability the sum is equal to 8.
2) P(X < 11) means the probability the sum is less than 11.
3) P(X > 14) means the probability the sum is greater than 14.

The answers:
1) P(X = 8) = 0
2) P(X < 11) = 6120 = 120
3) P(X > 14) = P(X = 15) = 12120 = 110