Clever counting » Permutations
Below you can find five examples of using permutations.
Example 1
How many flags, with 3 horizontal stripes, can be made if you can choose from three different colours, whereby every colour can only be used once?
Answer:
For the first stripe you can choose from 3 colours, for the second stripe you can choose from 2 colours and for the last stripe you can have only the 1 colour that is left.
See drawing:
 | 3 × 2 × 1 = 3! = 6 flags. |
Example 2
A secret code consists of 3 different digits.
You know that 0, 1 and 2 are not used in this code.
How many possible codes are there?
Answer:
For the first digit there are 7 possibilities, because you can use 3 to 9.
For the second digit you have 6 possibilities left, as you cannot use the same digit as for the first digit.
For the third digit you have 5 possibilities left.
See drawing:
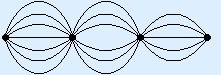 | 7 × 6 × 5 = 7 nPr 3 = 210 possibilities. |
Example 3
How many 'words' can be made from the letters in the Dutch word 'appeltaart'.
Answer:
You have 10 letters: a1p1p2elt1a2a3rt2
With which you can make 10! words.
See also example 1.
However, if you swap the a's with each other, what can be done in 3! ways, you will have the same word, because a1p1p2elt1a2a3rt2 is the same as a2p2p1elt2a3a1rt1.
The total number of words is therefore 3! = 6 times as small.
The same applies for the p and the t.
The total number of words is therefore: 10!3!2!2! = 151200
Example 4
On a shelf are 6 books, of which 4 cook books. In how many ways can you order these books when the cook books have to stand next to each other.
Answer:
The 4 cook books together just form one book, so you have 3 books in total which can be ordered in 3! ways. But with every way, the cook books can be ordered in 4! ways. The total number of ways is therefore 3! × 4! = 144.
Example 5
In how many ways can 4 boys and 5 girls sit in a row when the middle three always need to be girls.
Answer:
For the middle three girls you have 5 × 4 × 3 = 60 possibilities.
For every possibility you have to divide the remaining 4 boys and 2 girls, on the six open spaces.
This can be done in 6! ways. In total, there are 60 × 6! = 43200 possibilities.