Probability » Vase model
You have to know this already:
The theory about probabilities and combinations.
What is the vase model?
The vase model can only be used when there is no replacing. So the probabilities change over time. How this works is shown with the example below.
Example 1
Given is the vase below with 4 red and 6 blue marbles.
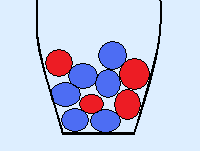
I take one marble marble without replacing it and repeat this another time.
The probability of getting a red marble the first time is 410.
There is a total of 10 marbles, of which 4 are red.
But the second time, the probability is not 410 anymore.
There is a total of 9 marbles, of which 3 are red. The probability is therefore 39.
The probability of taking two red marbles is 410 × 39 = 215.
The same probability can be calculated using combinations.
According to the definition of probability we have to divide the number of good outcomes by the total number of possible outcomes.
The easiest way is starting with the number of possible outcomes. The total number of outcomes can be calculated using 10 nCr 2. You take 2 of the 10 marbles.
Then you can calculate the good outcomes.
The different combinations possible to take 2 red marbles from 4 red marbles is 4 nCr 2. This has to be multiplied with the number of possible combinations to take 0 blue marbles from 6 blue marbles. That is 6 nCr 0.
This gives you the following calculation:
Probability = number of good outcomesnumber of possible outcomes =  4
4
2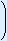
 6
6
0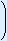
 10
10
2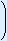 = 6 · 145 = 215
= 6 · 145 = 215
This calculation with combinations looks very tedious for this example, but is very useful for larger numbers.
Example 2
In this example a vase model is used for a lottery.
Let's say there is a lottery with 20 tickets.
There is one first price of 10 euros.
There are three second prices of 5 euros.
I have bought 3 tickets in this lottery.
What is the probability I win exactly 10 euros.
Answer:
The lottery can be pictured like this.
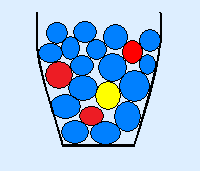
There are 20 tickets, so 20 marbles.
There is one first price, the yellow marble.
There are three second prices, the red marbles.
The rest of the marbles have no price, these are the blue marbles.
There are two possible ways to get 10 euros:
1. Winning first price and two times nothing.
2. Winning two second prices and once nothing.
Both probabilities have to be calculated and added together.
Probability =  1
1
1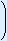
 16
16
2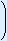
 20
20
3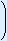 +
+
 3
3
2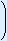
 16
16
1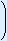
 20
20
3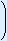 =
1 · 1201140 + 3 · 161140 = 1681140 = 1495
=
1 · 1201140 + 3 · 161140 = 1681140 = 1495