Vergelijkingen » Goniometrische vergelijkingen

De vergelijkingen sin(A) = C en cos(A) = C met C = –1, 0 of 1 los je op met de eenheidscirkel.

sin(A) = 0 geeft A = k · π
sin(A) = 1 geeft A = 12π + k · 2π
sin(A) = –1 geeft A = – 12π + k · 2π

cos(A) = 0 geeft A = 12π + k · π
cos(A) = 1 geeft A = k · 2π
cos(A) = –1 geeft A = π + k · 2π

De vergelijkingen sin(A) = C en cos(A) = C

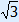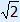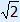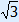
met C = –12wortel 3, – 12wortel 2, – 12, 12, 12wortel 2 of 12wortel 3  

los je op door uit de exacte-waarden-cirkel één oplossing B af te lezen.

Daarna gebruik je:
sin(A) = C geeft A = B + k · 2π  of  A = π – B + k · 2π
cos(A) = C geeft A = B + k · 2π  of  A = –B + k · 2π

Voorbeeld 1
sin(2x – 13π) = 1
2x – 13π = 12π + k · 2π
2x = 56π + k · 2π
x = 512π + kπ

Voorbeeld 2
cos2(x) – cos(x) = 0
cos(x) · (cos(x) – 1) = 0
cos(x) = 0  of  cos(x) = 1
x = 12π + kπ  of  x = k · 2π

Voorbeeld 3
2sin(3x) = 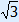wortel 3
sin(3x) = 12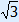wortel 3
sin(3x) = sin(13π)
3x = 13π + k · 2π  of  3x = π – 13π + k · 2π
x = 19π + k · 23π  of  x = 29π + k · 23π

Voorbeeld 4
2cos(2x – 13π) = –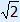wortel 2
cos(2x –13π) = –12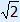wortel 2
cos(2x –13π) = cos(34π)
2x – 13π = 34π + k · 2π  of  2x – 13π = –34π + k · 2π
2x = 1312π + k · 2π  of  2x = –512π + k · 2π
x = 1324π + kx  of  x = –524π + kπ