Vergelijkingen » Inklemmen

Inklemmen is systematisch op zoek gaan naar het antwoord van een vergelijking door waarden in de formule in te vullen. Voor het oplossen van een vergelijking met behulp van inklemmen gebruik je het beste een grafiek voor de eerste schatting en daarna een tabel om te laten zien welk antwoord het dichtste bij het doel zit. Laat altijd zien welke uitkomst net boven en welke uitkomst net onder het doel zit.

Ik geef twee voorbeelden.
Bij het tweede voorbeeld leg ik uit hoe je meer decimalen kan berekenen.

Voorbeeld één formule
Gegeven is de formule b = 3p² + 4p.
Bereken, nauwkeurig op één decimaal, welke p hoort bij de uitkomst b = 150?

Antwoord
Maak de grafiek en zoek het punt dat bij b = 150 hoort.

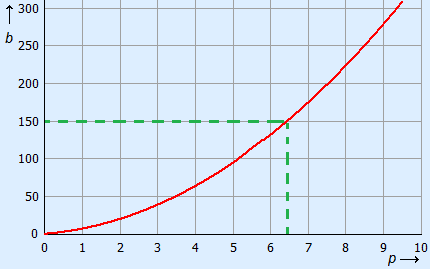
Zo te zien is dit p = 6,3.
Maak een tabel met voor p getallen net boven en onder je schatting en vul deze tabel verder in.

	p	6,1	6,2	6,3	6,4	6,5
	b	136,0	140,1	144,3	148,5	152,8
	verschil met 150	14,0	9,9	5,7	1,5	2,8

In de tabel is b = 148,5 het dichtst bij 150, dus de oplossing is p ≈ 6,4.

Dit vraagstuk had ook algebraïsch opgelost kunnen worden door de vergelijking 3p² + 4p = 150 op te lossen.

Voorbeeld twee formules
Karel en Tom laten allebei hun modelvliegtuigje opstijgen.
De hoogte h in meters van de vliegtuigjes na t seconden kun je berekenen met de volgende formules.
Karel: h = 0,1t² + 0,1t
Tom: h = 0,021t³
Bereken na hoeveel seconden de vliegtuigjes op dezelfde hoogte zijn. Rond af op één decimaal.

Antwoord
Maak de grafieken in één assenstelsel en schat de waarde van t van het snijpunt.

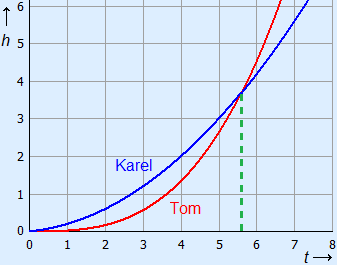
Zo te zien is dit t = 5,7.
Maak een tabel met voor t getallen net boven en onder je schatting en vul deze tabel verder in.

	t	5,5	5,6	5,7	5,8	5,9
	Karel: h = 0,1t2 + 0,1t	3,58	3,70	3,82	3,94	4,07
	Tom: h = 0,021t3	3,49	3,69	3,89	4,10	4,31
	verschil	0,09	0,01	0,07	0,16	0,24

Ik geef nadat ik de tabel gemaakt heb, altijd aan welke getallen groter zijn. Hierboven heb ik dat gedaan door ze vet te maken, maar op papier onderstreep ik ze meestal. Zo is het makkelijk te zien tussen welke twee waarden het snijpunt/omslagpunt ligt, namelijk tussen t = 5,6 en t = 5,7. Het verschil is het kleinste bij t = 5,6, dus de oplossing is t ≈ 5,6.

Meer decimalen?

Als er meer decimalen gevraagd worden, zal je nog een tabel moeten maken waarin je met meer decimalen werkt. Stel dat we bij het voorbeeld hierboven meer decimalen nodig hebben. We weten dat het snijpunt tussen t = 5,6 en t = 5,7 ligt. Verder weten we door het zeer kleine verschil dat we zojuist bij t = 5,6 hadden, dat dit net na 5,6 zal zijn. We maken dus een tabel met 5,60, 5,61, 5,62. Mocht het nodig zijn, maak je de tabel gewoon langer met 5,63, enzovoorts. Let op dat je de uitkomsten misschien ook op meer decimalen zal moeten geven.

	t	5,60	5,61	5,62
	Karel: h = 0,1t2 + 0,1t	3,696	3,7082	3,720
	Tom: h = 0,021t3	3,688	3,7077	3,728
	verschil	0,008	0,0005	0,008

De oplossing is t ≈ 5,61.

Op zich was het niet nodig geweest om het vierde decimaal te geven voor de uitkomsten van t = 5,61 in de tabel hierboven. Maar stel dat je nog meer decimalen nodig hebt voor je oplossing, weet je daardoor tenminste wel dat het snijpunt ligt tussen t = 5,61 en t = 5,62. Je maakt dan een nieuwe tabel met voor t de getallen tussen 5,61 en 5,62.