Meetkunde » Vierhoeken
Inhoud
- Onregelmatige vierhoek- Vierkant
- Rechthoek
- Parallellogram
- Vlieger
- Ruit
- Trapezium
Hoe zit de verzameling vierhoeken in elkaar?
Onregelmatige vierhoek
Een vierhoek zonder bijzondere eigenschappen. Er is geen symmetrie en er lopen geen lijnen evenwijdig/parallel aan elkaar.
De oppervlakte kan alleen berekend worden door inlijsten te gebruiken.
Vierkant (regelmatige vierhoek)
Een vierkant is een vierhoek met vier gelijke zijden en vier gelijke hoeken.
Bij een vierkant snijden de diagonalen elkaar middendoor en staan ze loodrecht op elkaar.
De diagonalen zijn even lang.
Er zijn twee paar evenwijdige lijnen.

| Oppervlakte | = lengte × breedte |
| = zijde × zijde | |
| = zijde2 |
Rechthoek
Een vierhoek met vier rechte hoeken.
Bij een rechthoek snijden de diagonalen elkaar middendoor en zijn ze even lang.
Oppervlakte = lengte × breedte
Parallellogram
Een vierhoek met draaisymmetrie.
Een vierhoek met twee paar evenwijdige zijden.
Tegenover elkaar liggende zijden zijn even lang (en evenwijdig).
Tegenover elkaar liggende hoeken zijn even groot.
De diagonalen delen elkaar middendoor.

Oppervlakte = basis × hoogte
Voorbeeld
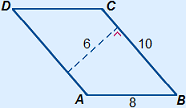
Basis en hoogte staan altijd loodrecht op elkaar.
Oppervlakte ABCD = 10 × 6 = 60
Vlieger
Een vlieger is een vierhoek waarvan een diagonaal een symmetrieas is.
Twee aan twee zijn de zijden van gelijke lengte.
De diagonalen staan loodrecht op elkaar.
Twee van de hoeken zijn van gelijke grootte.
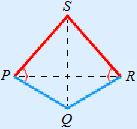
Oppervlakte = lengte diagonaal PR × lengte diagonaal QS : 2
Voorbeeld
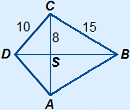
We hebben de lengte van beide diagonalen nodig.
AC = 2 × 8 = 16
De lengte van BD is echter niet gegeven, dus moeten we die berekenen. Dit kan met de stelling van Pythagoras.
DS = |
BS = | |||||||||||||||||||||||||||||||||
BD = DS + BS = 6 + 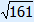
Oppervlakte ABCD = AC × BD : 2 = 16 × (6 + 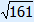 ) : 2 ≈ 149,5
) : 2 ≈ 149,5
Ruit
Een ruit is een vierhoek met vier gelijke zijden.
Een ruit is een vierhoek waarvan beide diagonalen symmetrieassen zijn.
Tegenover elkaar liggende hoeken zijn even groot.
De diagonalen staan loodrecht op elkaar en delen elkaar midden door.
De diagonalen delen de hoeken middendoor (deellijn/bissectrice).
Oppervlakte = zie vlieger
Trapezium
Een vierhoek waarin je één paar evenwijdige lijnen hebt.
Geen bijzondere eigenschappen.
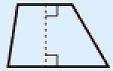
Oppervlakte = (lengte lange basis + lengte korte basis) × hoogte : 2
Voorbeeld
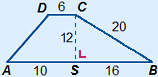
Basis en hoogte staan altijd loodrecht op elkaar.
AB = AS + BS = 10 + 16 = 26
Oppervlakte ABCD = (AB + CD) × CS : 2 = (26 + 6) × 12 : 2 = 192
Gelijkbenig trapezium
Wanneer de basishoeken van een trapezium even groot zijn, dan heet het trapezium gelijkbenig.
Heeft één symmetrieas.
Er zijn twee paar gelijke hoeken.
Twee zijden (blauw hieronder) zijn gelijk in lengte.
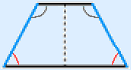
Oppervlakte = zie trapezium
Hoe zit de verzameling vierhoeken in elkaar?
Zie de figuur hieronder:
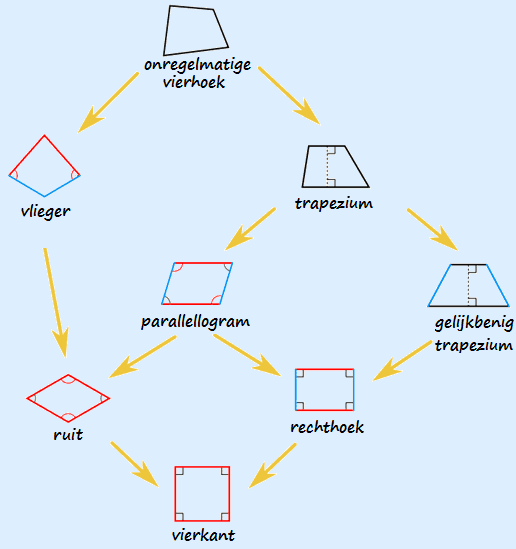
Een vierkant is een bijzondere rechthoek.
Een vierkant is een bijzondere ruit.
Een vierkant is een bijzonder parallellogram.
Een vierkant is een bijzondere vlieger.
Een vierkant is een bijzonder trapezium.
Een rechthoek is een bijzonder parallellogram.
Een rechthoek is een bijzonder trapezium.
Een ruit is een bijzonder parallellogram.
Een ruit is een bijzondere vlieger.
Een ruit is een bijzonder trapezium.
Een parallellogram is een bijzonder trapezium.
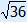 = 6
= 6