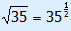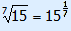Arithmetic » (Square) Roots
Inhoud
1. The square root2. Other roots
3. Exact or rounded off?
4. Root = power
1. The square root
It is often said that the square root is the reverse operation of squaring. That seems to be the case.
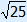 = 5, because 5 × 5 = 25
= 5, because 5 × 5 = 25
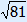 = 9, because 9 × 9 = 81
= 9, because 9 × 9 = 81
Why is the square root than not really the reverse of square?
Because (–5)2 = –5 × –5 is also 25, however 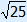 is always 5 (and not –5).
is always 5 (and not –5).
Example 1
You can use the square root when you need to calculate the side of a square when you know the area (A = s2).
Of a certain square the area is 56.25 cm2. The side is then  = 7.5 cm.
= 7.5 cm.
Example 2
The square root can also be used in equations: (See quadratic equations)
| x2 + 5 | = 25 |
| x2 | = 20 |
| x | = –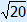 or x = or x = 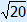 |
Negative numbers
Finding the square root of a negative number is impossible. You cannot find a number that multiplied with itself is negative. When asked for the square root of a negative number you write down: 'not possible'.
The square root of a negative number does exist when working with complex numbers.
2. Other roots
What if you do not need the 'reverse' of a square but of a higher power.
Lets say you are wondering which number to the power of 5 is 32768.
In that case you need the fifth root of 32768. That is 8.
| x5 | = 32768 |
| x | = 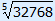 = 8 = 8 |
(In this case we do not have 'or x = –8', for (–8)5 = –32768)
From (–8)5 = –32768 you can deduct that the fifth root of –32768 should be –8 agian. Roots with an odd exponent of a negative number are possible.
3. Exact or rounded off?
The square root of 7 is not a whole number. There is no whole number multiplied with itself 7.
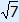 = 2.645751... (infinitely continuing).
= 2.645751... (infinitely continuing).
When working with this number within a calculation you can work with the exact 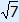 or with the rounded 2.65. When working with the last one, you will get rounding differences and therefore an approximation. Only round off at the end of your calculation and only if the exercise asks this of you.
or with the rounded 2.65. When working with the last one, you will get rounding differences and therefore an approximation. Only round off at the end of your calculation and only if the exercise asks this of you.
4. Root = power
You can also write a root as a power.
The rule is 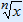 = x
= x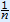 .
.
Examples