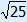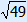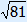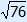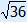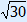Equations » Quadratic equations (x² = number / sum-product-method / the quadratic formula)

Recognise:

Quadratic equations can be divided into three categories.
Every category has its own way of solving the equation.

Category:	Examples:
Reducible to x2 = number	x2 = 25  or  x2 – 7 = 2
Reducible to binomial = 0	5x2 – x = 0 or 3x2 + 5x = x2 – 7x
Reducible to trinomial = 0	5x2 – 4x + 3 = 0 or 3x2 = 2x2 + 4x + 12

Directly to other theory within this page:

– Factorising formulas (incl. sum-product-method)
– The quadratic formula / abc-formula
– Completing the square
– Calculate the vertex
– Shape of the parabola
– Calculate the points of intersection with the axes
– Quadratic equations with a parameter
– More examples (mixed)

x² = number

Use the balance method or the card method to solve these equations.
Reduce to x² on the left-hand side and then find the square root.
REMEMBER: MOST OFTEN THERE ARE TWO SOLUTIONS!

Example 1 x2 = 25  x =   or x = – x = 5  or x = –5	Example 2 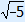x2 + 7  = 2  x2  = –5  doesn't exist:    no solutions
Example 3 –2x2 + 1  = –97  –2x2  = –98  x2  = 49  x =   or x = – x = 7  or x = –7	Example 4 (x + 3)2 + 5  = 86  (x + 3)2  = 81  x + 3 = –  or x + 3 =  x + 3 = –9  or x + 3 = 9 x = –12  or x = 6

Binomial = 0

Reduce to zero and factorise the binomial (single brackets). After factorising, either the left-hand factor or the right-hand factor must be zero.

Example 1 5x2 – x  = 0  x(5x – 1)  = 0 x = 0 or  5x – 1 = 0 x = 0 or  5x = 1 x = 0 or  x = 15

Example 2 3x2 + 5x  = x2 – 7x 2x2 + 12x  = 0  2x(x + 6)  = 0 2x = 0  or x + 6 = 0 x = 0  or x = –6

Trinomial = 0

Reduce to zero and then factorise the trinomial (double brackets). When factorising is not possible, use the quadratic formula / abc-formula or completing the square.

Example 1 2x2 + 4x + 12  = 3x2 –x2 + 4x + 12  = 0 x2 – 4x – 12  = 0 (x + 2)(x – 6)  = 0 x + 2 = 0  or x – 6 = 0 x = –2  or x = 6

Example 2 5x2 – 4x – 3 = 0 a = 5,  b = –4,  c = –3 D = (–4)2 – 4 · 5 · –3 = 76 x = –(–4) + 2 × 5 or  x = –(–4) – 2 × 5 x ≈ 1.27 or  x ≈ –0.47

Factorising

Single brackets (binomial)

Look for the greatest common divider in both terms.
That is what you write in front of the brackets.
Your factorised formula is always of the form y = …(… + …)  or  y = …(… – …).
Example: In both terms of y = 6x² + 15x you have a factor 3x
After all, the formula can be written as y = 2 × 3 × x × x + 3 × 5 × x.
This formula can therefore be factorised and written as y = 3x(2x + 5).

Sum-product-method (trinomials)

A sum is the answer of an addition and a product is the answer of a multiplication.
The sum-product-method can only be used with a trinomial that is
written as x² + bx + c = 0 (so a = 1).
Underneath this trinomial you write double brackets like this: (x … …)(x … …) = 0
Behind the x on the open spaces you have to fill in the two numbers that are added b and multiplied c. Write a + in front of positive numbers.

Example 1 x2 + 5x + 6 = 0 (x + 3)(x + 2) = 0 x = –3 or x = –2		Example 2 x2 – 6x + 9 = 0 (x – 3)(x – 3) = 0  x = 3
Example 3 15x2 + 15x – 6 = 0 get a = 1 by multiplying every term by 5   x2 + x – 30 = 0 (x – 5)(x + 6) = 0  x = 5 or x = –6		Example 4 5x2 + 25x – 70 = 0 get a = 1 by dividing every term by 5  x2 + 5x – 14 = 0 (x – 2)(x + 7) = 0  x = 2 or x = –7

Check factorising when you want to learn more about factorising.

The quadratic formula / abc-formula

This formula can be used to solve every quadratic equation.
However, only use it on trinomials that cannot be factorised, as it costs a lot of work.

The equation has to be written as ax² + bx + c = 0.
Find the numbers for a, b and c. Watch out with negative numbers!

With these numbers you first calculate the Discriminant, the formula is:
D = b² – 4ac
When D is negative, you have no solutions. 
When D is zero, you have one solution.
When D is positive, you have two solutions.

When D is not negative, use the following two formulas to calculate the values of x.
x = –b + 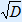2a or x = –b – 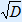2a

Watch out! On your calculator this might look like this:
(–b + 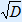) / (2 × a)

Do you want to know how this formula is derived?
Look at derivation of the quadratic formula.

Example 2 at 'Trinomial = 0' above and example 6 all the way at the bottom of the page are examples of the quadratic formula.

Completing the square

You can also solve a quadratic equation by completing the square. However, it is not necessary to learn this. After all, you can solve any quadtratic equation with the quadratic formula / abc-formula. Look at completing the square for the theory and a number of examples on how you can solve a quadratic equation by completing the square.

Calculate the vertex

Use x_vertex = –b2a.
To calculate y_vertexyou have to fill in x_vertexinto the formula.

Check vertices of parabolas for more information about calculating the vertex.

Shape of the parabola

Is completely determined by a.
When a = positive you have an upward-opening parabola
When a = negative you have a downward-opening parabola
The bigger the difference between a and zero, the narrower the parabola is.

Calculate the points of intersection with the axes

For the intersection with the y-axis, calculate y for x = 0.
For the intersections with the x-axis calculate x for y = 0.

Quadratic equations with a parameter

When you have an equation like 2x² + 5x + p = 0  or  –x² + 2x  + 1,5 = –4x + p, check quadratic equations with a parameter.

More examples (mixed)

Example 1 x2 – 5  = 31  x2  = 36  x =   or x = – x = 6  or x = –6	Example 2 (5 – 2x)2 = 81 5 – 2x =   or 5 – 2x = – 5 – 2x = 9  or 5 – 2x = –9 –2x = 4  or –2x = –14 x = –2  or x = 7
Example 3 2x2 =  8x  2x2 – 8x  = 0  2x(x – 4)  = 0 2x = 0 or x  – 4 = 0 x = 0 or x  = 4	Example 4 x(x + 2)  = 3 x2 + 2x  = 3 x2 + 2x – 3  = 0 (x + 3)(x – 1)  = 0 x + 3 = 0 or x  – 1 = 0 x = –3 or x  = 1
Example 5 (3x – 1)2  = (x – 7)2 3x – 1 = x – 7  or 3x – 1 = –(x – 7)  2x = –6  or 3x – 1 = –x + 7 x = –3  or 4x = 8 x = –3  or x = 2
Example 6 x2 + 7x + 9.5  = 19x – 2x2 3x2 – 12x + 9.5  = 0 a = 3,  b = –12,  c = 9.5 D = (–12)2 – 4 × 3 × 9.5 = 30 x = –(–12) + 2 × 3  or x = –(–12) – 2 × 3 x ≈ 2.91  or x ≈ 1.09

To top