Simplifying formulas » Completing the square
Where is it based on?
Completing the square is based on the rule:
(x + a)2 = (x + a)(x + a) = x2 + 2ax + a2
Let us have look at an example.
(x + 5)2 = (x + 5)(x + 5) = x2 + 2 × 5 × x + 52 = x2 + 10x + 25
Without the intermediate step:
(x + 5)2 = x2 + 10x + 25
You can clearly see that the number in front of x is two times 5 and the solitary number is the square of 5. By using this, we can also calculate 'backwards'.
Calculating backwards
Look at the following example.
x2 + 18x + 81 = (x + ...)2
You will probably quickly see that the number 9 is supposed to go on the dots. After all, two times 9 is the number in front of x and 9 squared is the solitary number.
x2 – 14x + 49 = (x + ...)2
Let's see. Two times the unknown number should be –14 and the unknown number squared should be 49. Therefore, the number –7 should be on the dots.
Where do you use this for?
We can rewrite a trinomial (of the form y = ax2 + bx + c) as a square. Which is a formula that is more beautiful and easier to work with.
Furthermore, it is easier to solve some quadratic equations.
Example
| x2 + 6x + 9 | = 25 |
| (x + 3)2 | = 25 |
x + 3 = –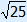 | or x + 3 = 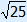 (you don't have to show this step) (you don't have to show this step) |
| x + 3 = –5 | or x + 3 = 5 |
| x = –8 | or x = 2 |
Most often the solitary number in the trinomial will not be the number you need to complete the square. Namely, this number should be the square of half the number in front of x. An extra intermediate step solves this problem nicely.
Example 1
| x2 – 20x – 10 | = 146 (both sides +110 to get the needed 100) |
| x2 – 20x + 100 | = 256 |
| (x – 10)2 | = 256 |
x – 10 = –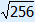 | or x – 10 = 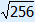 (you don't have to show this step) (you don't have to show this step) |
| x – 10 = –16 | or x – 10 = 16 |
| x = –6 | or x = 26 |
Example 2
| 2x2 + 24x + 100 | = 42 |
| x2 + 12x + 50 | = 21 (both sides –14 to get the needed 36) |
| x2 + 12x + 36 | = 7 |
| (x + 6)2 | = 7 |
x + 6 = –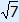 or or | x + 6 = 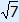 |
x = –6 – 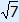 or or | x = –6 + 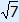 |