Equations » Card method

Contents

1. What is the card method?
2. How can you solve an equation using the card method?
3. Quadratic equations
4. How do I know where to put the card?


Note:

When you have an equation with a variable on both sides of the =-sign, you cannot use the card method.
When you have something like 3x + 5 = 7x – 2, check balance method.
When you have something like 5x2 + 3x = 2x + 4, check quadratic equations.

1. What is the card method?

The card method is a simple way of solving equations. It is much like the gapped exercises you had in primary school. On something you do not know you put a card. Calculate what number should be on your card. You copy what is on the card, and what number should be on the card.
At the end, you know the unknown value of the variable.


2. How can you solve an equation using the card method?

Follow the steps below:
1. Copy the equation to your notebook.
2. If necessary, shorten the formula.
3. Draw the card on what you want to know* and copy what is on the card underneath.
4. Calculate what number should be on the card.
5. Calculate the solution.
(6. Check your solution by filling in the solution in the formula)

* The correct spot to put the card is on the variable and what belongs to the variable according to the calculation rules. At section 4 below there is some more explanation on where to put the card.

Example 1
85 = 25 + 5a
5a = 60
  a = 605 = 12

Check:
25 + 5 × 12 = 85 		Example 2
170 – 14t = 72
14t = 98
  t = 9814 = 7

Check:
170 – 14 × 7 = 72


Example 3
3n – 12 = –34,5
3n = –22,5
  n = –22,53 = –712  

Check:
3 × –712 – 12 = –3412 		Example 4
5(4x – 8) + 3 = –107
5(4x – 8) = –110
4x – 8 = –22
4x = –14
  x = –144 = –312

Check:
5(4 × –312 – 8) + 3 = –107


3. Quadratic equations

The variable in the equation can only be on one side of the equation.
If it is not, look at quadratic equations.
Keep making intermediate steps using the card method until you are left with only the variable on one side.
Note: Most often you have two solutions!
The moment you get rid of the square, you will get two solutions.

Example 1
4 + 3x2 = 151 
3x2 = 147 
x2 = 49 
x = 7 or x = –7

Check:
4 + 3 × 72 = 151 		Example 2
–2x2 – 5 = –17 
–2x2 = –12 
x2 = 6 
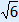x = square root(6) or x = –square root(6)

Check:
–2 × (square root(6))2 – 5 = –17


Example 3
–x2 + 3 = 8 
–x2 = 5 
x2 = –5 
no solutions  		 Example 4
(3x + 1)2 = 169 
3x + 1 = 13 or 3x + 1 = –13
3x = 12 or 3x = –14
x = 4 or x = –423

Check:
(3 × 4 + 1)2 = 169
(3 × –423 + 1)2 = 169

Example 5
(2x – 2)2 + 4 = 68 
(2x – 2)2 = 64 
2x – 2 = 8 or 2x – 2 = –8
2x = 10 or 2x = –6
x = 5 or x = –3

Check:
(2 × 5 – 2)2 + 4= 68
(2 × –3 – 2)2 + 4 = 68


4. How do I know where to put the card?

Of course you know the calculation order.
Always put the card on everything except that part of the formula you are supposed to do last according to the calculation order.

In example 1 of section 2, the formula is 40 + 5a.
Because we first have to multiply and then add the card is on everything but the number added.

In example 1 of section 3, the formula is 4 + 3x2.
Because we first have to square (power), then have to multiply and then have to add, the card is on everything but the addition. In the new intermediate step, you only have the square and the multiplication. The card has to be on the square and not on the multiplication.

In example 3 of section 3, the formula is (3x + 1)2.
According to the formula, you first have to multiply, then add and then you have to find the square. Therefore you have to get rid of the square first by putting the card on everything but the square. The card will be between the brackets. In the new intermediate step you have the multiplication and the addition. Because the addition has to be done the last, the card will be on everything but the addition.

Conclusion:
You are working through the calculation order in the formula in reversed order to solve the equation. This is even more visible in the reversed arrow chain method.


To top