Equations » Reversed arrow chain method

Note:

When you have an equation with a variable on both sides of the =-sign, you cannot use the reversed arrow chain method.
When you have something like 3x + 5 = 7x – 2, check balance method.
When you have something like 5x2 + 3x = 2x + 4, check quadratic equations.

Contents

1. Regular arrow chain
2. Reversed arrow chain with linear equations
3. Reversed arrow chain with quadratic equations

1. Regular arrow chain

If you want to work with a reversed arrow chain, you have to know how to make a normal arrow chain for a formula. You start with looking at the variable. What are the operations that have to be done with the variable. These operations you put on arrows. Of course in the order that they have to be done according to the formula. What has to be done first, according to the calculation rules will be on the first arrow.

Examples

Formula Arrow chain
y = 7x + 3 × 7 + 3
x pijl rechts … pijl rechts y
b = 3(a + 2) + 4  + 2 × 3 + 4
a pijl rechts … pijl rechts … pijl rechts b

2. Reversed arrow chain with linear equation

Linear equations do not have any powers (like squares) in the equation.

Rules

When you reverse an arrow chain, the following happens to the operators:
× becomes :
+ becomes –
: becomes ×
– becomes +

When you have an equation, you first make the normal arrow chain and then the reversed arrow chain. Calculate the solution with the reversed arrow chain.

Examples


Solve the equation: 4x + 12 = 104 

  Arrow chain 
will be:		 × 4 + 12
 x  pijl rechts  …  pijl rechts  104
 
Reversed
arrow chain 
will be:		 : 4 – 12
x pijl links … pijl links  104

Calculation: (104 – 12) : 4 = 23.
Answer: x = 23		 Solve the equations: 4(x + 12) = 104 

  Arrow chain 
will be:		 + 12 × 4
 x  pijl rechts  …  pijl rechts  104
 
Reversed
arrow chain 
will be:		 – 12 : 4
x pijl links … pijl links  104

Calculation: 104 : 4 – 12 = 14.
Answer: x = 14

Check

If you want you can check your solutions by filling in your answers in the formula.
Example 1: 4 × 23 + 12 = 92 + 12 = 104 and that is correct!
Example 2: 4 × (14 + 12) = 4 × 26 = 104 and that is correct!

3. Reversed arrow chain with quadratic equations

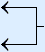
Works the same as with the linear equations except for the following:
The arrow for squared     reversed is a double arrow:
 #2 square root(hash mark) pijl links dubbel
pijl rechts –square root(hash mark)

Because, for example, –5 × –5 is also 25 you have two possible solutions for quadratic equations. When you have to find the square root of a negative number the equation has no solutions.

Example 1
Solve the equation: x2 + 5 = 41

  Arrow chain 
will be:		 #2 + 5
 x  pijl rechts  …  pijl rechts  41
 
Reversed
arrow chain 
will be:		 x = 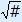square root(hash mark)

x = –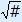square root(hash mark)		 pijl links dubbel … – 5pijl links
  41

Calculation: 41 – 5 = 36 en 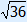square root(36) = 6
Answer: x = 6 of x = –6
Check: 62 + 5 = 36 + 5 = 41
Check: (–6)2 + 5 = 36 + 5 = 41

Example 2
Solve the equation: a2 – 5 = –10

  Arrow chain 
will be:		 #2 – 5
 a  pijl rechts  …  pijl rechts  –10
 
Reversed
arrow chain 
will be:		 a = 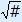squa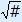re root(hash mark)

a = –square root(hash mark)		 pijl links dubbel … + 5pijl links
  –10

Calculation: –10 + 5 = –5 and 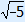square root(negative 5) = not possible.
Answer: no solutions


To top