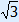Equations » Exponential equations

1. What is an exponential equation?
2. Solving using the card method
3. Solving using logarithms
4. Examples for the advanced

1. What is an exponential equation?

When you have the unknown variable in the exponent of a power, you have an exponential equation.

Examples
7 · 3^x = 567
3^2x – 4 = 27

2. Solving using the card method

Not everybody might call this the card method. If you do not know what is meant by the card method, check the theory about card method.

It works like this.
Write the right-hand side of the equation as a power with the same base as the left-hand side of the equation. After doing that, the two exponents must be equal to each other.
For that reason, you can put a card on the left-hand side exponent. This one is equal to the exponent in the right-hand side of the equation.

Examples

5^3x – 2	= 9765625
5^3x – 2	= 5¹⁰
(card on 3`x` – 2)
3`x` – 2	= 10
3`x`	= 12
`x`	= 4

2^2x + 1	= 2048
2^2x + 1	= 2¹¹
(card on op 2`x` + 1)
2`x` + 1	= 11
2`x`	= 10
`x`	= 5

5 · 3^1.5x + 2	= 1215
3^1.5x + 2	= 243
3^1.5x + 2	= 3⁵
(card on op 1.5`x` + 2)
1.5`x` + 2	= 5
1.5`x`	= 3
`x`	= 2

3. Solving using logarithms

It is not always possible to write the right-hand side of the equation as a power. In that case, you cannot use the card method as described above. Use logarithms instead.

It works like this:
We start with the equation: a^x = q
You can calculate x with a logarithm. Logarithm is always shortened to log.
a^x = q gives x = ^alog(q).

Calculator

On modern calculators it can probably be filled in like that.
On older calculators, you have to fill ^alog(q) in as log(q) : log(a)

^alog(q) can also be written like this: log_a(q)

Examples

3^x	= 1000
`x`	= ³`log`(1000)
`x`	≈ 6,29

3 + 5^x	= 2500
5^x	= 2497
`x`	= ⁵`log`(2497)
`x`	≈ 4,86

2^x + 5	= 700
`x` + 5	= ²`log`(700)
`x`	= ²`log`(700) – 5
`x`	≈ 4,45

On the calculator:
How this looks on the calculator, with the first example you will get log(1000)/log(3)

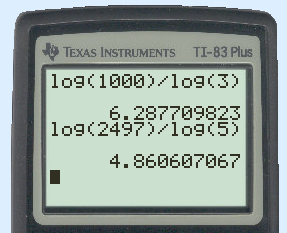
Check logarithms for more information about logarithms.

4. Examples for the advanced

Example 1

3^2x – 1	= 19
3^2x – 1	= 13² · 3^0,5
3^2x – 1	= 3^–2 · 3^0.5
3^2x – 1	= 3^–1.5
2`x` – 1	= –1.5
2`x`	= –0.5
`x`	= –0.25

Example 2

3 · (12)^x + 7	= 55
3 · (12)^x	= 48
(12)^x	= 16
(2^–1)^x	= 2⁴
2^–x	= 2⁴
–`x`	= 4
`x`	= –4

Example 3

3^x	= 9^x – 1
3^x	= (3²)^x – 1
3^x	= 3^2(x – 1)
3^x	= 3^2x – 2
`x`	= 2`x` – 2
–`x`	= –2
`x`	= 2

Example 4

3^x + 2 + 3^x	= 10
3² · 3^x + 3^x	= 10
9 · 3^x + 3^x	= 10
10 · 3^x	= 10
3^x	= 1
3^x	= 3⁰
`x`	= 0

Example 5

4^x – 1	= (12)^3x – 1
(2²)^x – 1	= (2^–1)^3x – 1
2^2(x – 1)	= 2^{–(3x – 1)}
2^2x – 2	= 2^–3x + 1
2`x` – 2	= –3`x` + 1
5`x` – 2	= 1
5`x`	= 3
`x`	= 35

Example 6

6 · (12)^x + 1	= 2^x
6 · 12^x + 1	= 2^x
Substitute: `p` = 2^x
6 · 1`p` + 1	= `p`
6 + `p`	= `p`²
–`p`² + `p` + 6	= 0
`p`² – `p` – 6	= 0
(`p` – 3)(`p` + 2)	= 0

`p` = 3 or	`p` = –2
2^x = 3 or	2^x = –2

x = ²log(3)
(2^x = –2 has no solutions)

Example 7

e^2x – e^x	= 0
e^2x	= e^x
2`x`	= `x`
`x`	= 0

Example 8

3`x` · e^x	= 12e^x
3`x` · e^x – 12e^x	= 0
e^x(3`x` – 12)	= 0

e^x = 0 or 3x – 12 = 0
e^x = 0 o r – 123x = 12
e^x = 0 o r – 123x = 4
(e^x = 0 has no solutions)