Formulas, graphs & relations » Asymptotes

An asymptote is a line, with which the graph will eventually coincide. In other words, a line that the graph will approach for very large values of one of the variables.

Horizontal asymptote

When you have a horizontal asymptote the formula for the asymptote will be: y = ... To find a horizontal asymptote you can fill in very large positive or negative numbers into the function. The (rounded) answer is the value the graph will approach, so that is the y-value of the asymptote.

Vertical asymptote

When you have an vertical asymptote the formula for the asymptote will be: x = ... To find a vertical asymptote you have to find the x-value for which the function has no outcome. With fractional functions this is the value of x for which the denominator is zero. With logarithmic functions this is the x-value, for which the expression between the brackets is equal to zero.

Below, you will find three examples. The graphs are given to help you, but these would not have been given if these were real exercises.

Example 1
Give the horizontal and vertical asymptote of the following function:

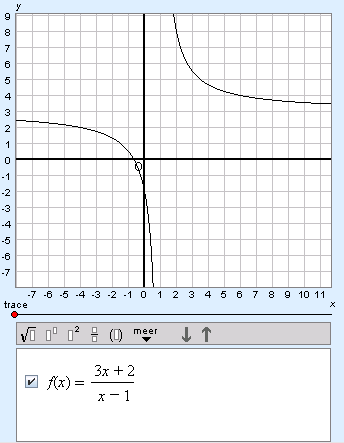
Filling in large positive and negative values into the formula will give outcomes approaching 3. The horizontal asymptote is y = 3. You cannot fill in 1 into the formula, because then you would have to divide by zero. The vertical asymptote is therefore x = 1.

Example 2
Give the horizontal asymptote of the following function:

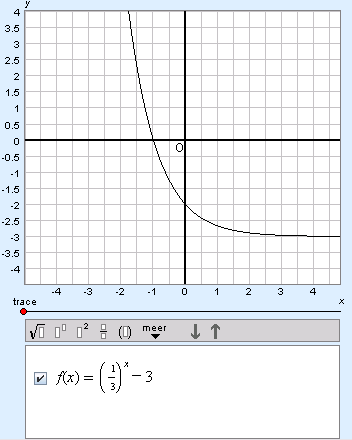
Filling in large positive and negative values into the formula will give outcomes approaching –3. The horizontal asymptote is y = –3. (The range of the function, every possible y-value, is everything greater than –3. In formal notation: y > –3)

Example 3
Give the vertical asymptote of the following function:

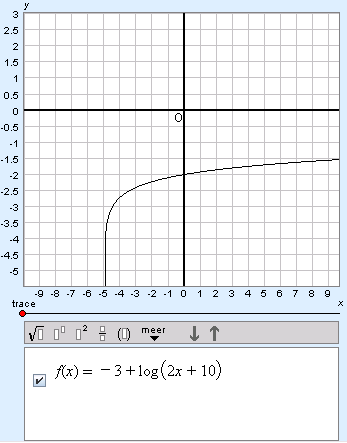
To find the vertical asymptote you need to solve the equation: 2x + 10 = 0.
The solution of this equation is x = –5.
The vertical asymptote is then x = –5.