Formulas, graphs & relations » Inversely proportional and hyperbolic relation
Contents
1. Inversely proportional relation2. Hyperbolic relation
3. Graph
4. Making formulas
1. Inversely proportional relation
If you make the value of x twice as big in an inversely proportional relation, the value of y will get twice as small.
The formulas can be used to calculate with area and sides, speed and distance, or dividing a certain amount in x parts.
Formula
Formulas that correspond to an inversely proportional relation are of the type x × y = c, with c a constant number.
This formula can be rewritten/rearranged to y = cx and x = cy.
Examples are y = 3x and a = –5b.
Table
The table below corresponds to an inversely proportional relationship.
| x | –6 | –5 | 2 | 3 | 4 |
| y | 5 | 6 | –15 | –10 | –7.5 |
The numbers in the top row can be multiplied with the numbers in the bottom row. Each outcome will be the same number, in this case –30. This is how you can recognize a table with an inversely proportional relation.
The formula for this table will therefore be y = –30x.
2. Hyperbolic relation
A formula in which the variable is in the denominator is called a fractional formula. A fractional formula corresponds to a hyperbolic relation.
An inversely proportional relation always has the variable in the denominator and is therefore also a hyperbolic relation.
Formula
A fractional formula is always of the type y = a + cx – b.
Examples of fractional formulas are y = 3 + 8x + 1 and T = 80 – 3t – 4.
3. Graph
The graph that corresponds to a hyperbolic relation is called a hyperbola.
Below you can see the graph of y = 2x (red) and the graph of y = 4 – 1x + 2 (blue).
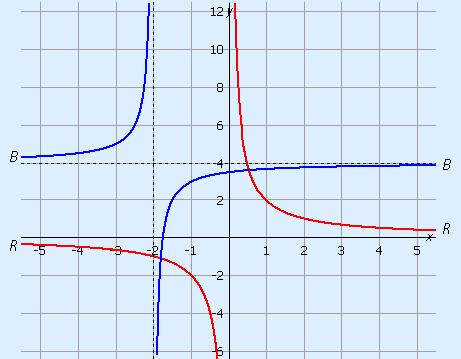
Because you cannot divide by 0, you will get asymptotes.
The red hyperbola has the asymptotes y = 0 and x = 0.
The blue hyperbola has the asymptotes y = 4 and x = –2 (the two dotted lines).
5. Making formulas
Inversely proportional
The formula is always of the type y = cx.
Example
| x | 1 | 4 | –2 | –3 |
| y | 24 | 6 | –12 | –8 |
In the table above y × x is always 24 so c = 24.
The formula is therefore y = 24x.
Hyperbolic relation / fractional formula
The formula is always of the type y = a + cx – b.
In this formula a is the y-value of the horizontal asymptote and b is the x-value of the vertical asymptote. To calculate c you need to solve an equation.
Example
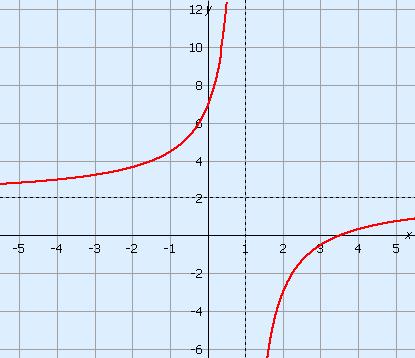
The asymptotes are y = 2 and x = 1. Fill these in for a and b.
The formula is then y = 2 + cx – 1.
Read off a point on the graph and fill it in the formula. For example (2, –3).
The equation will be:
| –3 | = 2 + c2 – 1 |
| –3 | = 2 + c |
| c | = –5 |
The formula is therefore y = 2 + – 5x – 1.
Slanted asymptote?
The explanation above also works for hyperbolic relations with an asymptote that is slanted. So if your asymptote, for example, follows the line y = 2x, you use 2x for a.