Formules, grafieken en verbanden » Domein en bereik
Voorkennis
Tekens
< betekent kleiner dan
> betekent groter dan
≤ betekent kleiner of gelijk aan
≥ betekent groter of gelijk aan
∞ betekent oneindig
≠ betekent niet gelijk aan
Interval
Een interval geeft een bepaald gebied op de getallenlijn aan.
| x < 5 | betekent dat x alle getallen kleiner dan 5 kan zijn. |
| x ≥ –7 | betekent dat x alle getallen groter of gelijk aan –7 kan zijn. |
| 3 ≤ x ≤ 8 | betekent dat x groter of gelijk aan 3, maar kleiner of gelijk aan 8 is. (x ligt tussen of is gelijk aan 3 en 8) |
| –2 ≤ x < 0 | betekent dat x groter of gelijk aan –2, maar kleiner dan 0 is. (x ligt tussen –2 en 0 of is gelijk aan –2) |
| 3 < x < 8 | betekent dat x tussen 3 en 8 ligt. |
| x < 3 of x ≥ 8 | betekent dat x kleiner is dan 3 of groter of gelijk aan 8. |
| x ≠ –7 | betekent dat x elk getal, behalve –7 kan zijn. |
Andere notaties
Soms worden intervallen in een andere notatie geschreven:
| Intervalnotatie | |||
| Ongelijkheid | Nederland | VS/VK | België |
| x < 5 | ⟨←, 5⟩ | (–∞, 5) | ]–∞, 5[ |
| x ≥ –7 | [–7, →⟩ | [–7, ∞) | [–7, ∞[ |
| 3 ≤ x ≤ 8 | [3, 8] | [3, 8] | [3, 8] |
| –2 ≤ x < 0 | [–2, 0⟩ | [–2, 0) | [–2, 0[ |
| 3 < x < 8 | ⟨3, 8⟩ | (3, 8) | ]3, 8[ |
| x < 3 of x ≥ 8 | ⟨←, 3⟩ of [8, →⟩ | (-∞, 3) of [8, ∞) | ]-∞, 3[ of [8, ∞[ |
| x ≠ –7 | ⟨←, -7⟩ of ⟨-7, →⟩ | (-∞, -7) of (-7, ∞) | ]-∞, -7[ of ]-7, ∞[ |
| elke x | ⟨←, →⟩ | (–∞,∞) | ]–∞, ∞[ |
Help: Ik zie vierkantjes in plaats van intervaltekens bij de NL notatie. Klik hier.
Domein
Het domein van een formule bestaat uit alle mogelijke waarden van x waarvoor de formule een uitkomst y geeft.
Of: Het domein van een functie bestaat uit alle mogelijke waarden van x waarvoor een functiewaarde bestaat.
Bereik
Het bereik van een formule bestaat uit alle mogelijke waarden voor y.
Of: Het bereik van een functie bestaat uit alle mogelijke functiewaarden.
Voorbeelden
Je kunt de grafiek bekijken door te klikken op 'Zie grafiek'.
De grafiek komt dan onder de tabel te staan.
| Formule | Domein | Bereik | |
| y = 3x + 5 | elke x | elke y | Zie grafiek |
| y = 3x2– 2 | elke x | y ≥ –2 | Zie grafiek |
y = 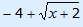 |
x ≥ –2 | y ≥ –4 | Zie grafiek |
y = 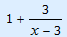 |
x ≠ 3 | y ≠ 1 | Zie grafiek |
y = 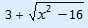 |
x ≤ –4 of x ≥ 4 | y ≥ 3 | Zie grafiek |
y = 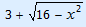 |
–4 ≤ x ≤ 4 | 3 ≤ y ≤ 7 | Zie grafiek |
Bij wortelverband staan ook nog drie voorbeelden.
