Geometry » Long diagonal
What is a long diagonal (cross-section)?
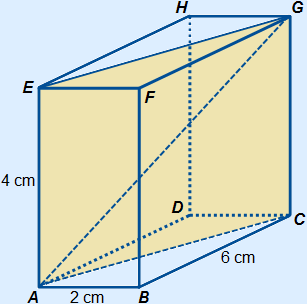
On the right you can see a cuboid. In this cuboid there is a cross-section drawn in with yellow. Because one of the long diagonals (AG) is in this cross-section, you may call this a long diagonal cross-section. Such a cross-section is always rectangular.
In this cuboid together with ACGE, long diagonal cross-section are also:
BDHF, BCHE, ADGF, DCFE en ABGH.
In total 6 possible long diagonal cross-sections.
As said in these cross-section you can draw the long diagonal. In this drawing AG. A long diagonal is a line between two vertices and travels through the figure. BH, CE and DF are also long diagonals of this cuboid.
How do you calculate the length of a long diagonal?
We again look at the cuboid above.
Let's assume we need to calculate AG.
Follow this algorithm with 4 steps:
| 1. | Find a long diagonal cross-section with the long diagonal in it. We are in luck, a usable long diagonal cross-section is already drawn. We could also use ABGH. | ||||||||||||||||
| 2. | Make a sketch of this cross-section and include the letters and given measurements.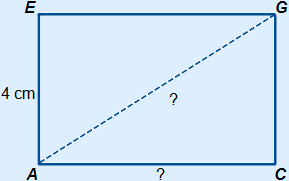 | ||||||||||||||||
| 3. | Find out which measurements you need before you can calculate the long diagonal. In this case we do not know AC, although we do need it. We can use Pythagoras to calculate AC.
AC = | ||||||||||||||||
| 4. | Calculate the length of the long diagonal. You have to use Pythagoras again:
AG = | ||||||||||||||||
How can you calculate another length within a cuboid?
What if you need to calculate the distance between C and the middle of side AE.
Check Pythagoras' theorem.
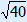
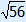 ≈ 7.48 cm
≈ 7.48 cm