Geometry » Pythagoras' theorem
Pythagoras' theorem is also known as Pythagorean theorem.
You can do Pythagoras' theorem:
1. With a scheme/table2. With the shortest/fastest way
3. With an equation.
Directly to the examples
More theory
4. Pythagoras in space5. Reverse Pythagoras' theorem (to check whether the angle is 90°)
All three methods use a2 + b2 = c2.
The theorem says that in a right-angled triangle the area of the two squares adjacent to the shorter sides added together is equal to the area of the area of the square adjacent to the longest side. In the figure below this means that the area of the two pink squares together is equal to the area of the blue square. The longest side is called the hypotenuse.
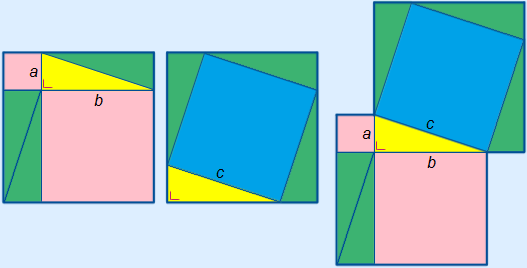
On the left, you can see that the pink area is the area of the whole square minus the four equal triangles. The area of the blue area is the same, also the area of the whole square minus the four equal triangles. On the right you can see those figures slid on top of each other in such a way that the yellow triangles are on top of each other. You now know that a2 + b2 = c2 must apply in the yellow triangle.
You can also say this:
In a right-angled triangle, the sum of the squares of the two shorter sides is equal to the square of the hypotenuse.
Misleading name
Contrary to what you might think, it was not Pythagoras who was the first to came up with this theorem. This method was already known with the Sumerians and Babylonians (current Iraq) and also the Indians long before Pythagoras lived. The Greek and perhaps Pythagoras are probably the one who brought the theorem to the western world.
1. With a scheme/table
Method that is used in most modern mathematics books.
Often used to teach it to pupils who get it for the first time.
Below you can see the scheme that is used for this method.
| side | square | ||
| shorter side | |||
| shorter side | + | ||
| hypotenuse | |||
| 1. | In the left column you fill in the sides that are known/given. Put a question mark at the side you need to calculate. REMEMBER: The hypotenuse should always be at the bottom! |
| 2. | Calculate the squares of the known sides (#2). |
| 3. | Calculate the square of the unknown side (by adding or subtracting). |
| 4. | Calculate the unknown side by using the 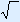 . . |
2. With the shortest/fastest way
Use Pythagoras' theorem in the following way:
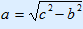
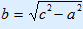
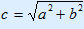
See examples.
3. With an equation
This method is used in some maths books and is probably the method your parents learned. You really use a2 + b2 = c2 in that form.
You fill in the known sides directly in the formula and then start solving the equation.
See examples.
Examples
|
Example 1 Calculate the length of the side with the '?'. So you have to calculate the hypotenuse. |
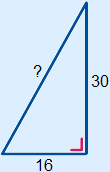 |
||||||||||||||||||||||||||||
| Scheme/table | Shortest/fastest | Equation | |||||||||||||||||||||||||||
1. Fill in 16 and 30 2. Calculate 256 and 900 3. 256 + 900 = 1156 4. ? = 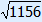 = 34 = 34 |
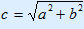 thus c = 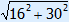 = 34
= 34 |
a2 + b2 = c2 thus
| |||||||||||||||||||||||||||
|
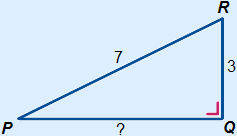
Example 2 Calculate the length of the side with the '?'. You have to calculate a shorter side. |
 |
||||||||||||||||||||||||||||
| Scheme/table | Shortest/fastest | Equation | |||||||||||||||||||||||||||
1. Fill in 3 and 7 2. Calculate 9 and 49 3. 49 – 9 = 40 4. PQ = 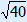 |
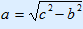 thus PQ = 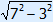 =
= 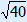 |
PQ2 + QR2 = PR2 thus
|
|||||||||||||||||||||||||||
Example 3 Given are the points A(–10, 3) and B(5, 23). Calculate the distance between these two points. You have to calculate the hypotenuse. First you need to calculate the horizontal and vertical distance between A and B. A and B are horizontally 5 – –10 = 15 and vertically 23 – 3 = 20 units apart. In a sketch it will look like this: 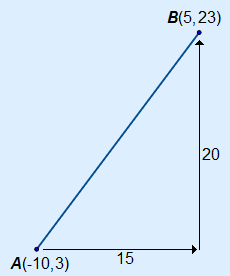 | |||||||||||||||||||||||||||||
| Scheme/table | Shortest/fastest | Equation | |||||||||||||||||||||||||||
1. Fill in 15 and 20 2. Calculate 225 and 400 3. 225 + 400 = 625 4. ? = 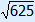 = 25 = 25 |
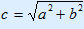 thus c = 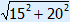 = 25 = 25 |
a2 + b2 = c2 thus
|
|||||||||||||||||||||||||||
4. Pythagoras in space
Within solids you often do not have any right-angled triangles. However, it is always possible to make your own, by using a cross-section. At the theory about long diagonals is an example of how you can calculate a long diagonal in a cuboid. It is also possible to use Pythagoras' theorem in other solids like pyramids and cones.
Example 1
In cube ABCD.EFGH with edges measuring 4, point K is in the middle of BC.
Calculate EK.
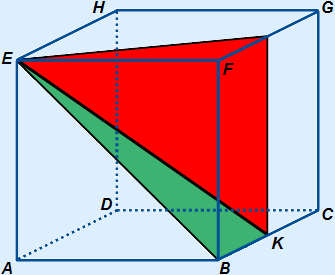
To calculate EK you will have to use right-angled triangles.
In the cube you see two possible right-angled triangles you can use.
Using the green cross-section:
We can calculate EK with right-angled triangle EBK.
BK = 2, but BE is unknown.
BE is calculable using the front face.
| Scheme/table | Shortest/fastest | |||||||||||||||||||||||||||||||||||
BE = |
BE = | BE = 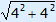 = = 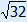 Now we can calculate EK. EK = | ||||||||||||||||||||||||||||||||||
Using the red cross-section:
We can calculate EK with right-angled triangle EKM.
KM = 4, but KM is still unknown.
EM is calculable using the top face.
| Scheme/table | Shortest/fastest | |||||||||||||||||||||||||||||||||||
EM = |
BE = | EM = 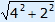 = = 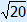 Now we can calculate EK. EK = | ||||||||||||||||||||||||||||||||||
Example 2
Pyramid ABCD.T has a square base with sides measuring 6 cm and slanted sides measuring 8 cm.
Calculate height ST.
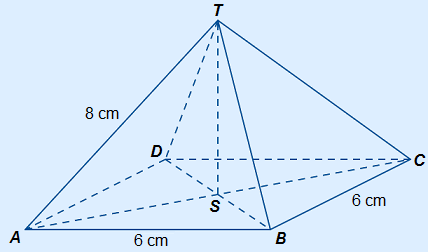
To calculate ST you can use cross-section ACT.
Sketch cross-section ACT with height ST.
You can see that SCT will be the needed right-angled triangle.
AC and SC are already written in the sketch below, however you need to calculate them first.
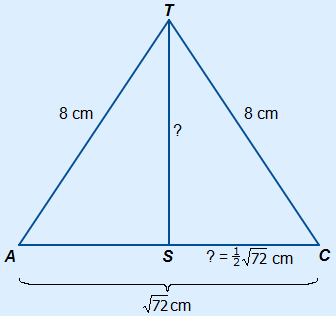
Calculate, using the base, the length of AC first.
With AC you can calculate the length of SC.
AC = |
SC is half the length of AC. |
|||||||||||||||||
Now you can calculate ST in triangle SCT.
| side | square | ||
SC = 12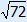 | 18 | ||
| ST = ? | 46 | + | |
| AC = 8 | 64 | ||
ST = 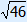 ≈ 6,78 cm
≈ 6,78 cm
5. Reverse Pythagoras' theorem
With the reverse of Pythagoras' theorem you can calculate/find out whether an angle in a triangle is greater than, less than or equal to 90°. With this method you always look at the angle opposite of the hypotenuse/longest side. In the newest maths books, this name might not be used. Although the method is explained.
It works like this:
Because a2 + b2 = c2 only works in a right-angled triangle you can use Pythagoras' theorem to check whether or not a triangle, of which you know all three sides, is right-angled or not. If not, you can also tell whether the triangle is acute-angled or obtuse-angled.
The rules:
a2 + b2 = c2. The triangle is right-angled.
a2 + b2 < c2. The triangle is obtuse-angled (c is too long and makes the angle bigger).
a2 + b2 > c2. The triangle is acute-angled (c is too short and makes the angle smaller).
Examples
 |
|
|
52 + 122 = 142 25 + 144 = 196 169 = 196 169 < 196 a2 + b2 < c2 So triangle ABC is obtuse-angled.  A > 90° A > 90°
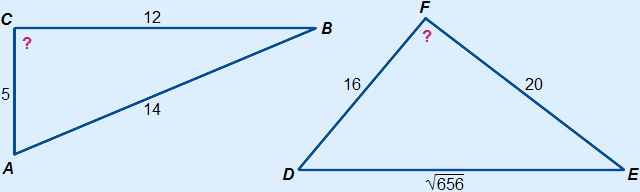
|
162 + 202 = (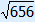 )2 )2256 + 400 = 656 656 = 656 a2 + b2 = c2 So triangle DEF is right-angled.  A = 90° A = 90°
|
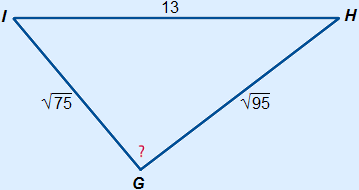 | |
(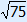 )2 + ( )2 + (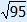 )2 = 132 )2 = 13275 + 95 = 169 170 = 169 170 > 169 a2 + b2 > c2 So triangle GHI is acute-angled.  A < 90° A < 90° | |
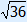 = 6
= 6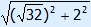 =
= 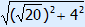 =
=