Geometry » Triangles

Click to go to area of a triangle


Types of triangles

There are all kinds of triangles. The biggest group are the irregular (or scalene) triangles. They do not have any special properties like a right angle or equal sides. These irregular triangles are divided into acute-angled triangles and into obtuse-angled triangles.

Right-angled triangle

A triangle with a right angle (90°).
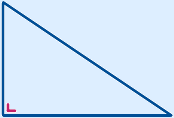
right-angled triangle
Note: Only in a right-angled triangle you can use Pythagoras' theorem and apply trigonometry (tan, cos and sin).

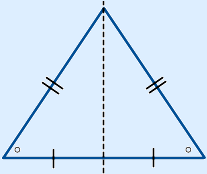
Isosceles triangle

A triangle with two sides equal in length. Because of this it has an axis of symmetry.
The angle that intersects the axis of symmetry is called the apex angle.
The other two angles are called the base angles. The base angles have the same size.
isosceles triangle with axis of symmetry drawn dotted

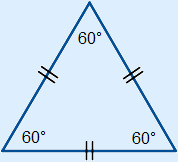
Equilateral triangle

A triangle with three equal sides. This triangle has three axes of symmetry.
The three angles in this triangle are all 60°.
equilateral triangle

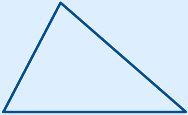
Acute-angled triangle

A triangle with three acute angles.
acute-angled triangle

Obtuse-angled triangle

A triangle with one obtuse angle and two acute angles.
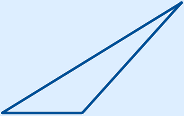
obtuse-angled triangle

Calculating the area

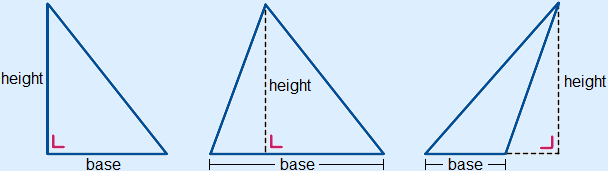
The area of a triangle can always be calculate with the formula:
Area = 12 × base × height  (or base × height : 2)
The base is always one of the sides of the triangle.
The height is the shortest distance between the chosen base and the opposite vertex. The height and base are always perpendicular to each other.

examples of triangles with base and corresponding height drawn in

The base can be any of the three sides. It does not have to be the bottom one. You can see this in the example below.

Are only the three sides known?
Use Heron's formula which is explained further below.

Example 1
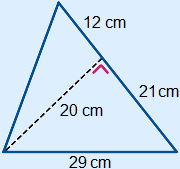
A triangle in wich three lengths are given. A sides of 29 and a side of 33 cm. The altitude from a vertex is 20 cm long and cuts the 33 cm side in two parts measuring 12 and 21.
The base is 21 + 12 = 33 cm.
The height is perpendicular to the base and is 20 cm.
Area = 12 × 33 × 20 = 330 cm2

Example 2
Calculate the area of triangle ABC.
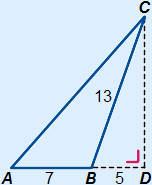
Obtuse-angled triangle ABC with AB=7, BC=13, BD(extension of AC)=5 and the altitude/height from C intersects AB in point D
The base is AB and the corresponding height is CD.
The height is not given, so has to be calculated using Pythagoras' theorem.

sidesquare
BD = 5  25 
CD = ?144+  
BC = 13169

 CD = 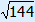square root(144) = 12
 Area ABC = AB × CD : 2 = 7 × 12 : 2 = 42

Heron's formula

When you only know the three sides, you can use Heron's formula.
This formula is sometimes called Hero's formula or the s-formula.
S is the semiperimeter.

Area = 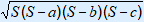square root(S(S-a)(s-b)(s-c))
With S = a + b + c2 and a, b and c the three sides.

Example 3
Calculate the area of triangle ABC.
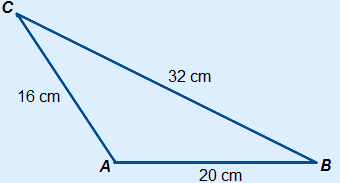
Triangle ABC with AB=20 cm, BC=32 cm and AC=16 cm
Calculate the semiperimeter first.
S = 20 + 32 + 162 = 34
Then use Heron's formula to calculate the area.
Area ABC = square root(34(34-20)(34-32)(32-16)) ≈ 130.9 cm2


To top