Geometry » Scale and scale factor

Contents

1. Calculating with a scale
2. Calculating with a scale factor
3. Scale factor with area and volume

For more information about enlargement, check similarity.

1. Calculating with a scale

When calculating with a scale you are always working with a drawing, map or photo. These are often smaller depictions of reality. To indicate how many times bigger this drawing should be in reality you can use a scale. A scale is a ratio.

A scale of 1:10 means that everything is in reality 10 times bigger. So 1 cm in the drawing is 10 cm in reality. A scale of 1:500 means that everything is in reality 500 times bigger. So 1 cm in the drawing is 500 cm = 5 m in reality.

In some rare cases the drawing is bigger than the reality. For example a louse that is shown enlarged in a biology book. The first number is still for the drawing and the second for the reality. A scale of 5:1 means that everything is in reality five times as small. In other words: 1 cm in the drawing is 0.2 cm in reality.

Pronunciation:
1:30 is pronounced as 1 to 30.

Example 1
On a map with a scale of 1:10 000 there is a road of 4.5 cm.
How many km is this road in reality?

Answer:
4.5 × 10 000 = 45 000 cm = 450 m = 0.45 km.

Example 2
On a drawing with a scale of 1:150 there is a meadow measuring 3 cm by 5.5 cm.
What is the area in m² in reality?

Answer:
Length = 5,5 × 150 = 825 cm = 8.25 m
Width = 3 × 150 = 450 cm = 4.5 m
Area = 8.25 × 4.5 = 37.125 m²

2. Calculating with a scale factor

Instead of using a scale you can also work with a scale factor.
A scale factor of 3 means that something will have to be three times as big.
Remember never to round off in the middle of your calculation. Only the final answer may be rounded off.

Example 1
A photo with a length of 10 cm and a height of 15 cm is being enlarged to a poster. The length of the poster will be 45 cm. What will be the height of the poster?

Answer:
The scale factor from photo to poster will be 45 : 10 = 4.5
The height will be 15 × 4.5 = 67.5 cm

Example 2
A tree with a height of 5 m is being drawn by someone (to scale).
In the drawing the tree is 10 cm high. The stem in the drawing is 1.5 cm wide.
How wide is the stem in reality?

Answer:
The scale factor from drawing to tree is is 500 : 10 = 50.
The stem is therefore 1.5 × 50 = 75 cm wide.

3. Scale factor with area and volume

If a figure is enlarged by a factor of five, the length will be five times greater, the width will be five times greater and the height will be five times greater.
The area will therefore be five times five times greater.
The volume will therefore be five times five times five times greater.

So:
Scale factor length = k
Scale factor area = k²
Scale factor volume = k³

Example 1
A photo with an area of 150 cm² will be enlarged by a factor of 7.
What will be the area of the enlargement?

Answer:
The scale factor for the area will be 7².
New area = 7² × 150 = 7350 cm².

Example 2
Exactly 27 cubes fit in a certain box.
Someone finds this box too small and orders a new box.
This new box is the old box enlarged by a factor of 2.
How many cubes will fit in the new box?

Answer:
The scale factor for the volume will be 2³.
So 2³ × 27 = 216 cubes will fit in the new box.

Example 3
An enlargement is being made of a photo.
The bicycle in the photo is 5 cm high. The area of the photo is 130 cm².
The enlargement will have an area of 4680 cm².
What height will the bicycle have in the enlargement?

Answer:
The scale factor for the area is 4680 : 130 = 36.
The scale factor for the length is then 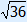 = 6 (you go back from k² to k).
The height of the bicycle in the enlargement is 5 × 6 = 30 cm.

Example 4
Someone is making an enlargement of a jug. The new jug fits 30 times more water.
What was the scale factor?

Answer:
k³ = 30
k = 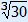 ≈ 3.1

To top