Inequalities » Quadratic inequalities

When solving a quadratic inequality, you solve the corresponding equation first, to calculate the point(s) of intersection. Just like with linear inequalities.
Then you decide on the solution using a sketch or the number line.

You have to know the meaning of the different signs being used.
If necessary, check domain and range for theory about intervals.

Example 1
a² + 30 < –11a + 2
a² + 30 = –11a + 2
a² + 11a + 28 = 0
(a + 4)(a + 7) = 0
a = –4 or a = –7

Continue with sketch

Continue with number line

There are two points of intersection and the graph is a upward-opening parabola. That gives you this sketch: 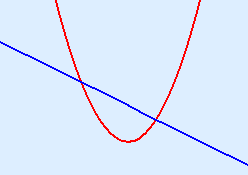Look to the original inequality: a2 + 30 < –11a + 2 Parabola < line That is in between the points of intersection. Solution: –7 < a < –4

Calculate whether or not the inequality is correct for numbers outside and in between the solutions. Outside the points of intersection: Take for example a = –8. (–8)2 + 30  < –11 × –8 + 2 94  < 90 Inc orrect! In between the two solutions: Take for example a = –6. (–6)2 + 30  < –11 × –6 + 2 66  < 68 Co rrect! You may sketch a number line to help you. 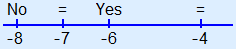Because 'in between' is correct, the solution is: –7 < a < –4

Example 2

–2x2 – 4x – 69	≤ –28x – 5
–2x2 – 4x – 69	= –28x – 5
–2x2 + 24x – 64	= 0
x2 – 12x + 32	= 0
(x – 4)(x – 8)	= 0
x = 4 of x =	8

Continue with sketch

Continue with number line

There are two points of intersection and the graph is a downward-opening parabola. That gives you this sketch: 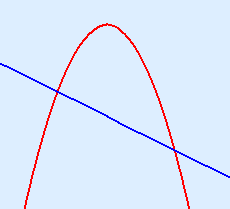Look to the original inequality: –2x2 – 4x – 69  ≤ –28x – 5  parabool  ≤ lijn That is outside the points of intersection! Solution: x ≤ 4 or x ≥ 8

Calculate whether or not the inequality is correct for numbers outside and in between the solutions. Outside the points of intersection: Take for example x = 2. –2 × 22 – 4 × 2 – 69  ≤ –28 × 2 – 5 –85  ≤ –61 Co rrect! In between the two solutions: Take for example x = 5. –2 × 52 – 4 × 5 – 69  ≤ –28 × 5 – 5 –139  ≤ –145 Inc orrect! You may sketch a number line to help you. Because 'outside' is correct, the solution is: x ≤ 4 or x ≥ 8

Watch out with:

No intersections (see sketch) Parabola < line or parabola ≤ line Solution: for every value of x Parabola > line or parabola ≥ line Solution: for no value of x
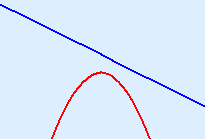One point of intersection/tangent* (see sketch) *A tangent in this context is the point where the graphs touch. Parabola < line Solution: x ≠ 1 (Every value of x except x = 1) Parabola > line Solution: for no value of x Parabola ≤ line Solution: for every value of x Parabola ≥ line Solution: x = 1	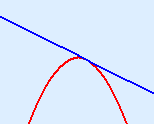tangent at x = 1