Trigonometry » Unit circle

In the text below all examples are in degrees.
Of course radians can also be used.


What is a unit circle?

The unit circle is a circle with centre O(0, 0) and a radius of 1.
Image of the unit circle as described above.

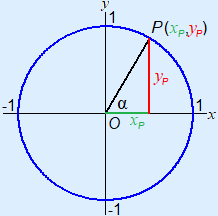
You can draw a point P on the unit circle. The angle of line OP with the horizontal axis, is called α (alpha). Some books use θ (theta). Here, the horizontal axis is always the positive part, so from the origin to (1, 0). If you consider P a moving point, you can also call the angle the rotation angle. This angle always starts at the horizontal axis and goes anti-clockwise. Is your angle going clockwise? Then your rotation angle is negative. So you are rotating backwards.
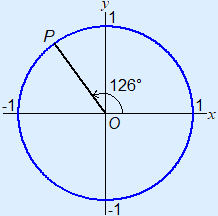
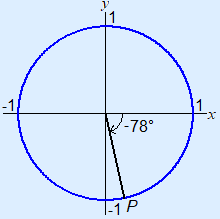
     Image of a unit cirlce with point P at 126° including line OP       Image of a unit circle with point P at -78° including line OP.

Coordinates

Point P of course has coordinates.
We write these as (xP, yP).
You can see this in the following example, where 0° < α < 90°.
     Image of a unit circle, with point P and line OP. The horizontal distance (xp) and the vertical distance (yp) to point P from the origin are also drawn.

How can you calculate in a unit circle?

Look at the example above. You can recognise a right-angled triangle and within this right-angled triangle you can use sine, cosine and tangent. Because of the radius of the circle, the hypotenuse is always 1. Using this, you will get the following calculations:
cos(α) = adjacenthypotenuse = xPOP = xP1 = xP
sin(α) = oppositehypotenuse = yPOP = yP1 = yP
tan(α) = oppositeadjacent = yPxP
tan(α) = oppositeadjacent = sin(α)cos(α)

Therefore:
xP = cos(α)
yP = sin(α)

We looked at an example in which 0° < α < 90°.
For α ≤ 0 or α ≥ 90° these formulas also apply.
See the examples below.

Example 1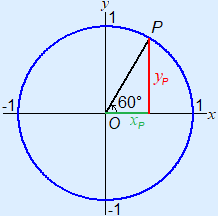
Image of a unit circle with point P with angle 60°.
xP = cos(60°) = 0.5
yP = sin(60°) ≈ 0.866


           Example 2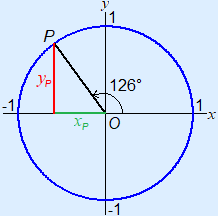
Image of a unit circle with point P with angle 126°.
xP = cos(126°) ≈ –0.588
yP = sin(126°) ≈ 0.809


Example 3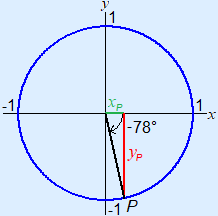
Image of a unit circle with point P with angle -78°.
xP = cos(–78°) = 0.208
yP = sin(–78°) ≈ –0.978 		           Example 4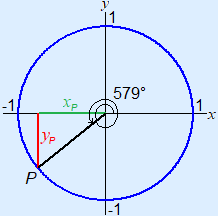
Image of a unit circle with point P with angle 579°.
xP = cos(579°) ≈ –0.777
yP = sin(579°) ≈ –0.629

In example 4 you can see that when α > 360° the formulas work as well.
As 579° – 360° = 219° you could also do cos(219°) ≈ –0.777 here.

Calculating the angle

When α has to be calculated and xP or yP is known you can use the inverse cosine and sine to calculate the angle. On your calculator you have to use cos–1 and sin–1.

Example 5
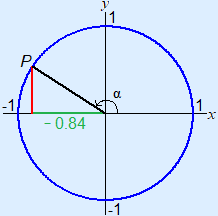
Image of a unit circle with point P and xp = -0.84. P lies in the second quadrant.
α = cos–1(–0.84°) ≈ 147°

However, cos–1 always gives an outcome between 0° and 180°. In the next example xP is also –0.84 although we have different rotation angle. Use symmetry to calculate the angle.

Example 6
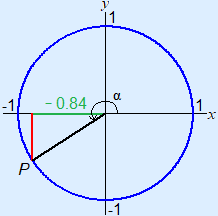
Image of a unit circle with point P and xp = -0.84. Now P lies in the third quadrant.
cos–1(–0.84°) ≈ 147° (see example above)
α ≈ 360° – 147° = 213°

yP can also be given. Then you have to use sin–1. This will give a result between –90° and 90°. Do you need a different angle? Calculate the angle like in the example above, using symmetry.

Example 7
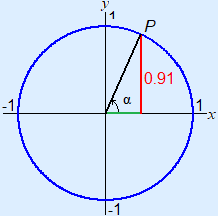
Image of a unit circle with punt P and yp = 0.91. P lies in the first quadrant.
α = sin–1(0.91°) ≈ 66°

Example 8
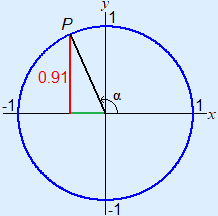
Image of a unit circle with point P and yp = 0.91. Now P lies in the second quandrant.
sin–1(0.91°) ≈ 66° (see example above)
α ≈ 180° – 66° = 114°


To top