Geometry » Angles
Contents
1. Angle types2. Measuring angles
3. Calculating angles
4. Vertically opposite angles
5. F-angles and Z-angles
6. Radian
7. Gradian
1. Angle types
An angle consists of a vertex and two arms. These arms make a certain angle with each other. The smaller the angle, the 'sharper' the intersection between the lines. The angle is a measurement/quantity that tells you what kind of intersection there is between two lines. When you extend the arms, the angle will not change.
The unit is degrees (°) or radians (rad).
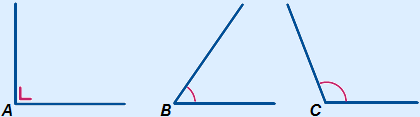
Right angle
A right angle is 90°. The two lines are perpendicular to each other.
A below is a right angle. There are two different indicators for a right angle.
Those are 
and 
.
Acute angle
An angle between 0° and 90° is an acute angle. B below is an acute angle.
Obtuse angle
An angle between 90° and 180° is an obtuse angle. C below is an obtuse angle.
Straight angle
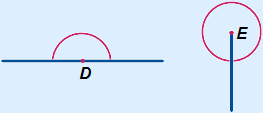
A straight angle is 180°. D below is a straight angle.
Full rotation
A full rotation is an angle of 360°. E below is a full rotation. A full rotation can also be called a full turn.
Reflex angle
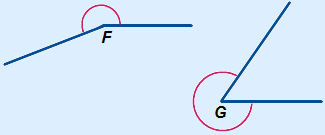
A reflex angle is an angle between 180° and 360°. F and G below are examples of reflex angles.
2. Measuring angles
With the compass rose
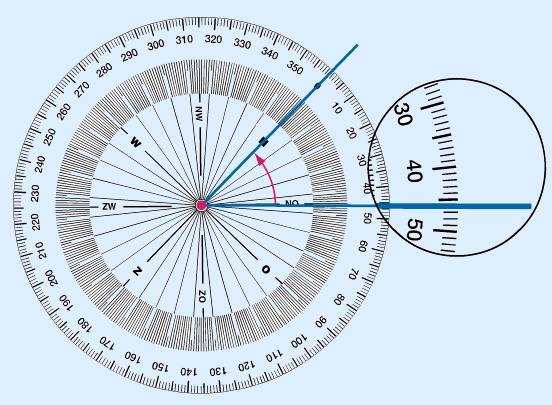
Put the dot in the centre of the compass rose exactly in the vertex. Put the 0 (or N) on one of the arms. Always make sure you can read off from the compass rose clockwise. In the example above you can read off that the angle is 46°.
Use this notation: A = 56°
With the geo-triangle
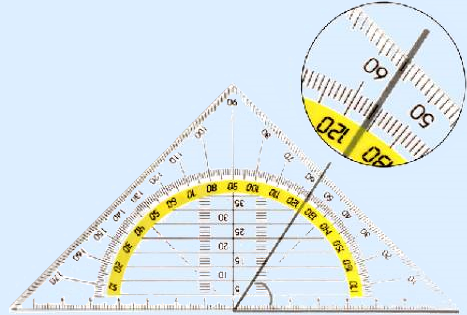
Put the geo-triangle on the angle with the longest side alongside one of the arms. Make sure the vertex is at the 0 of the longest side of the geo-triangle. Now you can read off two values at the other arm. In the example above these are 56° and 124°. You can see that the angle is acute so the correct answer is 56°.
Another way is the fact that you start measuring at the arm where the longest side of the geo-triangle is alongside. You start counting there at 0°, continue with 10°, 20° etc. You then know which protractor you need and you can read off the correct value.
Use this notation: A = 56°
3. Calculating with angles
Straight angles
A straight angle is 180°. The angles that form a straight angle together are therefore 180° together.
Example
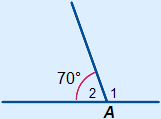
A1 = 180° – 70° = 110°
Triangle
The three angles in a triangle add up to 180°.
Example
In a triangle it is known that there is an angle of 68° and an angle of 34°.
What size is the third angle?
Answer: 180° – 68° – 34° = 78°
See triangles for angle properties in certain triangles.
Quadrilateral
In every quadrilateral the four angles add up to 360°.
Example
In a quadrilateral it is known that there are two angles of 37° and one angle of 130°.
What size is the fourth angle?
Answer: 360° – 37° –37° – 130° = 156°
See quadrilaterals for angle properties in certain quadrilaterals.
Polygon / n-gon
In a polygon with n angles, the total number of degrees can be calculated using:
total number of degrees = (n – 2) × 180°.
Example
What size is every angle in a regular 15-gon (pentadecagon)?
Answer: Total number of degrees = (15 – 2) × 180° = 2340°.
There are fifteen vertices so every angle is 2340° : 15 = 156°.
4. Vertically opposite angles
If two straight lines intersect it creates vertically opposite angles.
Vertically opposite angles are equal in size.
Example
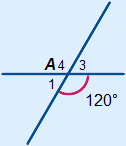
A2 = A4 = 120°
A1 = A3 = 180° – 120° = 60°
5. F-angles and Z-angles
With F-angles and Z-angles we mean angles that are the same because two parallel lines are intersecting these vertices.
Because of Z-angles: A = B and C = D.
Because of F-angles: E = F
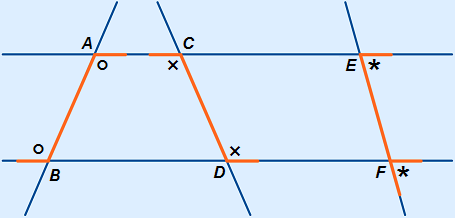
Example
In triangle ABC it is given that DE is a mid-parallel (so DE // AB).
It is also known that A2 = 38°, D2 = 104° and E1 = 50°.
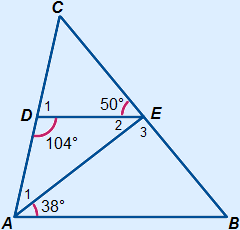
Calculate all the other angles:
| B | = E1 = 50° (F-angles) |
| A2 | = E2 = 38° (Z-angles) |
| E3 | = 180° – 38° – 50° = 92° |
| A1 | = 180° – 38° – 104° = 38° |
| D1 | = 180° – 104° = 76° |
| C | = 180° – 76° – 50° = 54° |
6. Radian
Another unit to measure angles is the radian. This is the SI-unit.
SI stands for 'Système international d'unités' which you can probably guess the English translation for. Those are the standard units.
In the word radian you probably recognise the first part of radius. The unit is derived from the radius.
Definition:
A radian is the size of the centre angle of a circle sector of which the length of the arc is equal to the length of the radius.
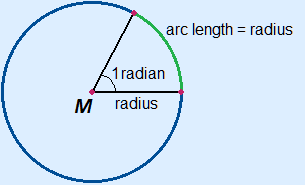
One radian is approximately 57.29577951°.
The word radian is often shortened to rad, although usually even rad is omitted.
So 1 rad ≈ 57.29577951°.
Because the angle depends on the length of the arc you have to do with the circumference of the circle. When looking at the unit circle (a circle with radius = 1) you have a circumference of 2π.
It follows that a full circle is 2π rad = 360°.
Half a circle is therefore an angle of π rad = 180°.
Converting radians and degrees
Above you have read that π rad = 180°.
With this you can easily calculate one rad and one degree:
1 rad = 180°π ≈ 57.29577951°
1° = π180° ≈ 0.01745329 rad
Formulas:
angle in radians = angle in degrees × π180°
angle in degrees = angle in radians × 180°π
Calculator
The calculator can often be set to calculate with degrees or radians. Press the SETUP or MODE button, sometimes you have to press more than once. You will get the option to choose between Deg(ree), Rad(ian) and sometimes Gra(dian).
7. Gradian
The gradian is another unit for measuring angles. The gradian is sometimes called decimal degree. The abbreviation for this unit is gon. Gonia is the Greek word for angle.
It has been created by the French because you can use the SI-prefixes (e.g. kilo, deci and centi). However, the use of this unit has never become common.
A circle consists of 400 gon. A right angle is 100 gon.
As this is a multiple of 10, you can use the SI-prefixes.
As 360400 = 0.9 it is rather easy to convert between degrees and gradians. To convert between radians and gradians change the 180° in the formulas above into 200.