Meetkunde » Hoeken

Inhoud

1. Soorten hoeken
2. Hoeken meten
3. Rekenen met hoeken
4. Overstaande hoeken
5. F-hoeken en Z-hoeken
6. Radialen
7. Decimale graden

1. Soorten hoeken

Een hoek bestaat uit een punt en twee benen. Die twee benen maken een bepaalde hoek met elkaar. Des te kleiner de hoek, des te scherper de lijnen snijden.
De hoek is een maat die aangeeft in welke mate de twee lijnen elkaar snijden. Als je de benen langer maakt, verandert er niets aan de hoek.
De eenheid is graden (°) of radialen (rad).

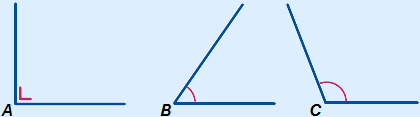
Rechte hoek

Een rechte hoek is 90°. Twee lijnen die 'haaks' of loodrecht op elkaar staan vormen een rechte hoek. hoekteken A hieronder is een rechte hoek.
Er zijn twee tekens om aan te geven dat een hoek recht is. Dit zijn Loodrecht door vierkantje en Loodrecht door extra loodrecht hoekje .

Scherpe hoek

Een hoek tussen 0° en 90° is een scherpe hoek. hoekteken B hieronder is een scherpe hoek.

Stompe hoek

Een hoek tussen 90° en 180° is een stompe hoek. hoekteken C hieronder is een stompe hoek.
Een rechte, scherpe en stompe hoek

Gestrekte hoek

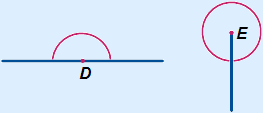
Een gestrekte hoek is 180°. hoekteken D hieronder is een gestrekt hoek.

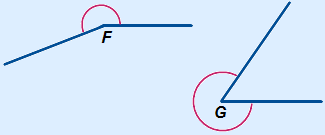
Inspringende of overstrekte hoek

Een inspringende hoek is een hoek tussen 180° en 360°.
hoekteken F en G hieronder zijn voorbeelden van een inspringende hoek.
Een inspringende hoek wordt ook wel een overstrekte hoek genoemd.
Twee inspringende of overstrekte hoeken

Volle hoek

Een volle hoek is 360°. hoekteken E hieronder is een volle hoek.
Een gestrekte en een volle hoek

2. Hoeken meten

Met de kompasroos

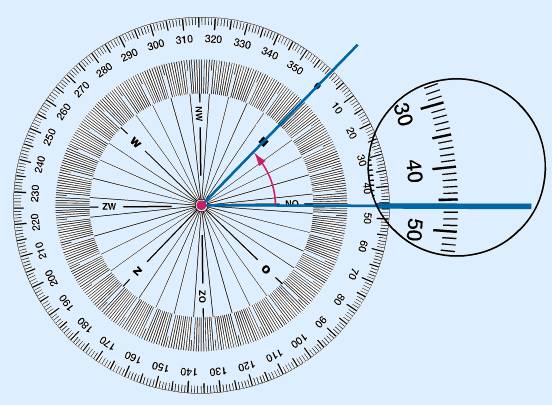
Leg de 0° (of N) op één van de benen. Het midden van de kompasroos moet precies op het punt liggen waar de benen samenkomen. Zorg altijd dat je met de klok mee kan aflezen onder hoeveel graden het andere been zich bevind.
In het voorbeeld hierboven kan je aflezen dat deze hoek 46° is.
Let op de notatie: hoekteken A = 46°

Met de geodriehoek

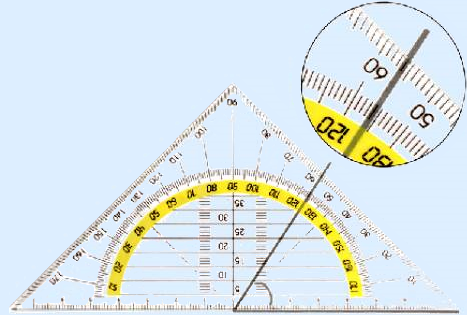
Leg je geodriehoek met de langste zijde langs één van de benen, zodat de geodriehoek zelf boven op het andere been ligt.
Zorg dat het hoekpunt precies bij de 0 op de langste zijde van de geodriehoek ligt.
Er zijn nu twee maten die je kunt aflezen bij het andere been.
In bovenstaand voorbeeld is dat 56° of 124°.
Bedenk dat deze hoek scherp is en dus 56° moet zijn.
Een andere manier is bij het eerste been (waar de langste zijde langs ligt) beginnen met tellen bij 0°. Je gaat dan via 10°, 20° enzovoort naar het andere been toe.
Let op de notatie: hoekteken A = 56°

3. Rekenen met hoeken

Gestrekte hoeken

Omdat een gestrekte hoek 180° is, moeten de hoeken die samen een gestrekte hoek vormen bij elkaar opgeteld 180° zijn.

Voorbeeld
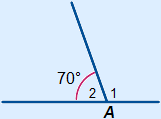
Gestrekte hoek verdeeld in hoek A1=onbekend en hoek A2=70° hoekteken A₁ = 180° – 70° = 110°

Driehoek

In een driehoek zijn de drie hoeken samen 180°.

Voorbeeld
In een driehoek heb je een hoek van 68° en van 34°.
Hoe groot is de derde hoek?
Antwoord: 180° – 68° – 34° = 78°
Zie ook driehoeken voor hoekeigenschappen in de verschillende driehoeken.

Vierhoek

In elke vierhoek zijn de vier hoeken samen 360°.

Voorbeeld
In een vierhoek zijn twee hoeken van 37° en één van 130°.
Hoe groot is de vierde hoek?
Antwoord: 360° – 37° –37° – 130° = 156°
Zie ook vierhoeken voor hoekeigenschappen in de verschillende vierhoeken.

Veelhoek

In een veelhoek met n hoeken, geldt voor het totaal aantal graden van de veelhoek totaal aantal graden = (n – 2) × 180°.

Voorbeeld
Hoe groot is elke hoek in een regelmatige 15-hoek?
Antwoord: Totaal aantal graden = (15 – 2) × 180° = 2340°.
Je hebt 15 hoeken dus per hoek heb je 2340° : 15 = 156°.

4. Overstaande hoeken

Als twee rechte lijnen elkaar snijden ontstaan overstaande hoeken.
Overstaande hoeken zijn even groot.

Voorbeeld
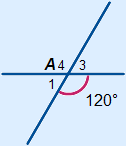
Twee rechte lijnen die snijden in punt A, hoek A1=120°
hoekteken A₂ = A₄ = 120°
A₁ = A₃ = 180° – 120° = 60°

5. F-hoeken en Z-hoeken

Met F-hoeken en Z-hoeken bedoelen we hoeken die gelijk zijn aan elkaar doordat er twee evenwijdige lijnen de hoekpunten snijden.

Vanwege Z-hoeken geldt: hoekteken A = B en C = D.
Vanwege F-hoeken geldt: E = F
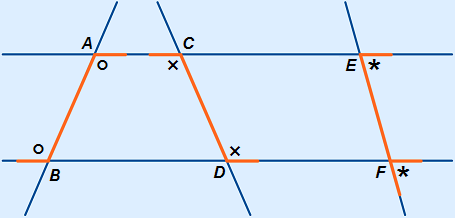
Twee evenwijdige lijnen met A, C en E op een lijn en B, D en F op de andere, ook is lijn AB, CD en EF getekend

Voorbeeld
In driehoek ABC geldt dat DE een middenparallel is. Dat wil zeggen dat DE // AB.
Verder is gegeven dat hoekteken A₂ = 38°, D₂ = 104° en E₁ = 50°.
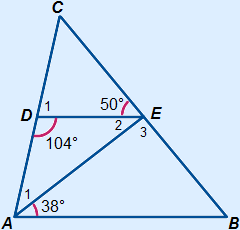
De hierboven omschreven driehoek, lijn AE is ook getekend
Bereken alle andere hoeken:

`B`	= `E`₁ = 50° (F-hoek)
`A`₂	= `E`₂ = 38° (Z-hoek)
`E`₃	= 180° – 38° – 50° = 92°
`A`₁	= 180° – 38° – 104° = 38°
`D`₁	= 180° – 104° = 76°
`C`	= 180° – 76° – 50° = 54°

6. Radialen

Een andere eenheid voor hoeken is de radiaal. Dit is de SI-eenheid.
SI staat voor 'Système international d'unités' wat Frans is voor het 'Internationale stelsel van eenheden'. Dit zijn standaardeenheden die zijn afgesproken.

In het woord radiaal, herken je vast al het eerste deel van radius. Radius is een ander woord voor straal. De eenheid is namelijk afgeleid van de straal.

Definitie:
Een radiaal is de grootte van de middelpuntshoek van een cirkelsector waarvan de lengte van de boog gelijk is aan de lengte van de straal.

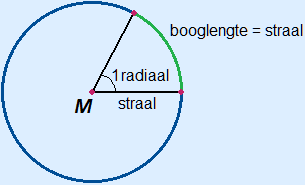
Cirkel waarin bovenstaande definitie weergegeven wordt

Eén radiaal is ongeveer 57,29577951°.
Het woord radiaal wordt meestal afgekort naar rad. Vaak wordt rad ook weggelaten.
Dus 1 rad ≈ 57,29577951°.

Omdat de grootte van de hoek afhangt van de boog op de cirkel heb je te maken met de omtrek van de cirkel. Kijk je in de eenheidscirkel (cirkel met straal = 1) dan heb je een omtrek van 2π.
Hieruit volgt dat helemaal rond een hoek is van 2π rad = 360°.
Half rond is dus een hoek van π rad = 180°.

Omrekenen tussen radialen en graden

Hierboven heb je gezien dat π rad = 180°.
Met deze gegevens kan je gemakkelijk één rad en één graad uitrekenen:
1 rad = 180°π ≈ 57,29577951°
1° = π180° ≈ 0,01745329 rad

Formules:
hoek in radialen = hoek in graden × π180°
hoek in graden = hoek in radialen × 180°π

Rekenmachine

De rekenmachine kan je meestal zo instellen dat deze met graden of met radialen rekent. Kijk onder de knop SETUP of MODE, soms moet je meerdere keren op MODE drukken. Je kan dan meestal kiezen tussen Deg(ree), Rad(ian) en soms Gra(dian). Dit zijn de Engelse benamingen van graden, radialen en decimale graden.

7. Decimale graden

De decimale graad is nog een andere eenheid om de grootte van een hoek uit te drukken. In het Engels heet deze eenheid 'gradian'. De afkorting van deze eenheid is gon. Gonia is het griekse woord voor hoek.
Ontworpen door de Fransen omdat met deze eenheid de SI-voorvoegsels (bijvoorbeeld kilo, deci en centi) gebruikt konden worden. Echter is het gebruik ervan nooit gemeengoed geworden.

Een cirkel bestaat uit 400 gon. Een rechte hoek is 100 gon.
Omdat je dan een veelvoud van 10 hebt, kan je de SI-voorvoegsels gebruiken.
Omdat 360400 = 0,9 kan je makkelijk omrekenen tussen graden en decimale graden. Voor het omrekenen tussen radialen en decimale graden gebruik je 200 in bovenstaande formules in plaats van 180°.

Naar boven