Trigonometry » Law of cosines

Note: The length a and the angle size α (alpha) are used both, look closely at the difference between the two letters.

Contents

What is the law of cosines?
How do you calculate with the law of cosines?
Proof of the law of cosines
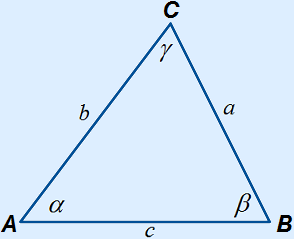
Triangle with letters at correct location as shown below

What is the law of cosines?

The law(s) of cosines for triangle ABC in which α = angle signA, β = angle signB, γ = angle signC, a = BC, b = AC and c = AB is:

a2 = b2 + c2 – 2bc cos(α)
b2 = a2 + c2 – 2ac cos(β)
c2 = a2 + b2 – 2ab cos(γ)

How do you calculate with the law of cosines?

With the law of cosines you can calculate the third side when you know two sides and the angle in between. You can also calculate the angles when you only know the three sides.

Example 1
Given is the following triangle. Calculate the unknown length.
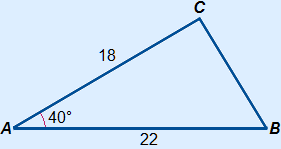
Triangle with a=? b=18 c=22 and α=40°

Answer:
We have to calculate a so we use a2 = b2 + c2 – 2bc cos(α)

Filling in the equation and solving it gives:
a2 = 182 + 222 – 2 × 18 × 22 cos(40°) ≈ 201.29...
a = BC = 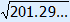square root(201.29...) ≈ 14.2


Example 2
Given is the following triangle. Calculate β.
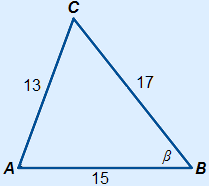
Triangle with a=17 b=13 c=15

Answer:
We have to calculate β so we use b2 = a2 + c2 – 2ac cos(β)

Filling in the equation and solving it gives:

132 = 172 + 152 – 2 × 17 × 15 × cos(β)
169 = 514 – 510 cos(β)
510 cos(β) = 345
cos(β) = 345510
β = 47.4°

Proof of the law of cosines

To prove the law of cosines, we use an altitude.
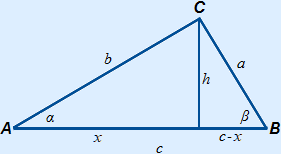
Triangle ABC with altitude h from C drawn, c is divided into x left of the altitude and c-x to the right of the altitude

The length of x can be calculated as follows:
x = b cos(α)

Because of Pythagoras' theorem the following is also true:
h2 = b2 – x2
h2 = a2 – (c – x)2

Therefore:

b2 – x2 = a2 – (c – x)2
b2 – x2 = a2 – (c2 – 2cx + x2)
b2 – x2 = a2 – c2 + 2cx – x2
b2 = a2 – c2 + 2cx
b2 – a2 = –c2 + 2cx
–a2 = –b2 – c2 + 2cx
a2 = b2 + c2 – 2cx

When we substite x for b cos(α) we will get:
a2 = b2 + c2 – 2bc cos(α)


To top